Πρέπειdimplak έγραψε: 60.
Απάντηση:ή
ή
ή
 αφού
αφού  για κάθε
για κάθε 
Αν
 η εξίσωση ισοδύναμα γίνεται:
η εξίσωση ισοδύναμα γίνεται:
Με

Με

Όλες ικανοποιούν την εξίσωση
Συντονιστής: exdx
Πρέπειdimplak έγραψε: 60.
Απάντηση:ή
ή
ή
 αφού
αφού  για κάθε
για κάθε 
 η εξίσωση ισοδύναμα γίνεται:
η εξίσωση ισοδύναμα γίνεται:


dimplak έγραψε: 60.
Απάντηση:ή
ή
ή



dimplak έγραψε: 67.
Απάντηση:
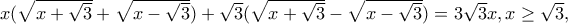


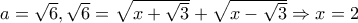
Kαλησπέρα Δημήτρηdimplak έγραψε: 51.
Απάντηση:





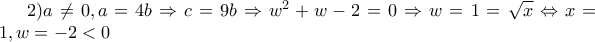
Kαλησπέρα Δημήτρη τρίτωσε το κακό....εννοώ κάποιο σκορ ...ξέρεις εσύ και προφανώς σε αστειεύομαι .....dimplak έγραψε: 66.
Απάντηση:ή
ή

Κάνουμε τις πράξεις και έχουμε:dimplak έγραψε: 62.
Απάντηση:
![5x^3+68=18\sqrt{5x-1}\sqrt[3]{x-1}+27x 5x^3+68=18\sqrt{5x-1}\sqrt[3]{x-1}+27x](/forum/ext/geomar/texintegr/latexrender/pictures/330f866b2abbdd811c65a41593a1b48f.png)
![\sqrt[3]{x-1}\geq 0 \sqrt[3]{x-1}\geq 0](/forum/ext/geomar/texintegr/latexrender/pictures/f49793edf8d172bae53bd035526356f7.png) άρα
άρα 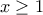
 (1) με ισότητα όταν
(1) με ισότητα όταν  , δηλαδή όταν
, δηλαδή όταν 
![x-1+1+1=x+1\geq 3\sqrt[3]{(x-1)\cdot 1\cdot 1} x-1+1+1=x+1\geq 3\sqrt[3]{(x-1)\cdot 1\cdot 1}](/forum/ext/geomar/texintegr/latexrender/pictures/abf093238c1ff66f80c8723f95d3e73d.png) (2) με ισότητα όταν
(2) με ισότητα όταν  , δηλαδή όταν
, δηλαδή όταν 
![(5x+8)(x+1)\geq 2\sqrt{9(5x-1)}\cdot 3\sqrt[3]{(x-1)}\Leftrightarrow (5x+8)(x+1)\geq 2\sqrt{9(5x-1)}\cdot 3\sqrt[3]{(x-1)}\Leftrightarrow](/forum/ext/geomar/texintegr/latexrender/pictures/c49e544c4f01305fb79794173ad87ab5.png)
![5x^2+13x+8\geq 2\sqrt{9(5x-1)}\cdot 3\sqrt[3]{(x-1)}\Leftrightarrow 5x^2+13x+8\geq 2\sqrt{9(5x-1)}\cdot 3\sqrt[3]{(x-1)}\Leftrightarrow](/forum/ext/geomar/texintegr/latexrender/pictures/402c7aa17397f35c9bc8fb8c2e1ed2ab.png)
![5x^2+40x+8\geq 2\sqrt{9(5x-1)}\cdot 3\sqrt[3]{(x-1)}+27x 5x^2+40x+8\geq 2\sqrt{9(5x-1)}\cdot 3\sqrt[3]{(x-1)}+27x](/forum/ext/geomar/texintegr/latexrender/pictures/b510c4ed8ec5051fd9e0ff287a1723f9.png) (3)
(3)
 , όπου
, όπου  θετικός πραγματικός. Έχουμε:
θετικός πραγματικός. Έχουμε:
 (4) με ισότητα όταν
(4) με ισότητα όταν 
 (5) με ισότητα όταν
(5) με ισότητα όταν  .
.  με ισότητα όταν
με ισότητα όταν  .
.  με ισότητα όταν
με ισότητα όταν  (6)
(6)![5x^3+68\geq 5x^2+40x+8\geq 2\sqrt{9(5x-1)}\cdot 3\sqrt[3]{(x-1)}+27x\Leftrightarrow 5x^3+68\geq 5x^2+40x+8\geq 2\sqrt{9(5x-1)}\cdot 3\sqrt[3]{(x-1)}+27x\Leftrightarrow](/forum/ext/geomar/texintegr/latexrender/pictures/734bd61e3695df117a7046932576dbdf.png)
![5x^3+68\geq 2\sqrt{9(5x-1)}\cdot 3\sqrt[3]{(x-1)}+27x=18\sqrt{5x-1}\sqrt[3]{x-1}+27x 5x^3+68\geq 2\sqrt{9(5x-1)}\cdot 3\sqrt[3]{(x-1)}+27x=18\sqrt{5x-1}\sqrt[3]{x-1}+27x](/forum/ext/geomar/texintegr/latexrender/pictures/05501d0923a19007068b857962704d95.png) , με ισότητα όταν
, με ισότητα όταν  .
. 
Η δοθείσα εξίσωση γράφεταιdimplak έγραψε: 65.
Απάντηση:

 μηδενίζουν το δεύτερο μέλος στην αρχική εξίσωση ,με πρώτο μέλος θετικό άρα δεν είναι δεκτές .
μηδενίζουν το δεύτερο μέλος στην αρχική εξίσωση ,με πρώτο μέλος θετικό άρα δεν είναι δεκτές .
Kαλημέρα Δημήτρηdimplak έγραψε: 68.
Απάντηση:ή

Πρέπειdimplak έγραψε: 69.
Απάντηση:ή
 .
. , ισχύει ότι
, ισχύει ότι 

 είναι αρνητική. Άρα οι μόνες λύσεις είναι
είναι αρνητική. Άρα οι μόνες λύσεις είναι  ή
ή  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες