39. viewtopic.php?f=21&t=33050&p=152929#p152929
40. Να λύσετε την εξίσωση
![\left[ {\sqrt {{{(1 + x)}^3}} - \sqrt {{{(1 - x)}^3}} } \right]\sqrt {2(1 + \sqrt {1 - {x^2}} )} = 5x \left[ {\sqrt {{{(1 + x)}^3}} - \sqrt {{{(1 - x)}^3}} } \right]\sqrt {2(1 + \sqrt {1 - {x^2}} )} = 5x](/forum/ext/geomar/texintegr/latexrender/pictures/6dacdd0d30ff02010e6e322fbb087b93.png)
Συντονιστής: exdx
![\left[ {\sqrt {{{(1 + x)}^3}} - \sqrt {{{(1 - x)}^3}} } \right]\sqrt {2(1 + \sqrt {1 - {x^2}} )} = 5x \left[ {\sqrt {{{(1 + x)}^3}} - \sqrt {{{(1 - x)}^3}} } \right]\sqrt {2(1 + \sqrt {1 - {x^2}} )} = 5x](/forum/ext/geomar/texintegr/latexrender/pictures/6dacdd0d30ff02010e6e322fbb087b93.png)
![\left[ {\sqrt {{{(1 + x)}^3}} - \sqrt {{{(1 - x)}^3}} } \right]\sqrt {2(1 + \sqrt {1 - {x^2}} )} = 5x:\left( 1 \right),\left( { - 1 \le x \le 1} \right) \left[ {\sqrt {{{(1 + x)}^3}} - \sqrt {{{(1 - x)}^3}} } \right]\sqrt {2(1 + \sqrt {1 - {x^2}} )} = 5x:\left( 1 \right),\left( { - 1 \le x \le 1} \right)](/forum/ext/geomar/texintegr/latexrender/pictures/cb018206923ad3d0c62679ec2d4ccf40.png)
 ,οπότε έχουμε
,οπότε έχουμε \displaystyle{\left[ {\sqrt {{{(1 + x)}^3}} - \sqrt {{{(1 - x)}^3}} } \right]\sqrt {{{\left( {\sqrt {1 + x} } \right)}^2} + {{\left( {\sqrt {1 - x} } \right)}^2} + 2\sqrt {1 + x} \sqrt {1 - x} } = 5x}
\displaystyle{\left[ {\sqrt {{{(1 + x)}^3}} - \sqrt {{{(1 - x)}^3}} } \right]\sqrt {{{\left( {\sqrt {1 + x} } \right)}^2} + {{\left( {\sqrt {1 - x} } \right)}^2} + 2\sqrt {1 + x} \sqrt {1 - x} } = 5x} \displaystyle{\Leftrightarrow 2\left( {{a^3} - {b^3}} \right)\sqrt {{{\left( {a + b} \right)}^2}} = 5\left( {{a^2} - {b^2}} \right)}
\displaystyle{\Leftrightarrow 2\left( {{a^3} - {b^3}} \right)\sqrt {{{\left( {a + b} \right)}^2}} = 5\left( {{a^2} - {b^2}} \right)}
 \displaystyle{\left( {a + b} \right)\left( {a - b} \right)\left( {2\left( {{a^2} + ab + {b^2}} \right) - 5} \right) = 0 \Leftrightarrow
\displaystyle{\left( {a + b} \right)\left( {a - b} \right)\left( {2\left( {{a^2} + ab + {b^2}} \right) - 5} \right) = 0 \Leftrightarrow \mathop \Leftrightarrow \limits^{\left( {a + b > 0} \right)} \left( {a = b \vee 2\left( {{a^2} + ab + {b^2}} \right) - 5 = 0} \right) \Leftrightarrow}
\mathop \Leftrightarrow \limits^{\left( {a + b > 0} \right)} \left( {a = b \vee 2\left( {{a^2} + ab + {b^2}} \right) - 5 = 0} \right) \Leftrightarrow}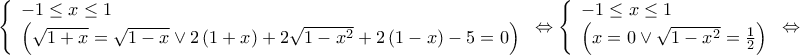

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες