Α)Αν
 διακεκριμένοι ακέραιοι τότε να δείξετε ότι το πολυώνυμο
διακεκριμένοι ακέραιοι τότε να δείξετε ότι το πολυώνυμο δεν γράφεται υπό την μορφή
δεν γράφεται υπό την μορφή 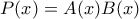 όπου τα
όπου τα  πολυώνυμα με ακέραιους συντελεστές και τουλάχιστον πρώτου βαθμού
πολυώνυμα με ακέραιους συντελεστές και τουλάχιστον πρώτου βαθμούB)Αν οι διαιρέσεις του
 με τα
με τα  δίνουν αντίστοιχα υπόλοιπα
δίνουν αντίστοιχα υπόλοιπα  δείξτε ότι : το
δείξτε ότι : το  είναι παράγοντας του
είναι παράγοντας του  και το
και το  είναι παράγοντας του πολυωνύμου
είναι παράγοντας του πολυωνύμου  Έστω τώρα ότι ισχύουν :
Έστω τώρα ότι ισχύουν :  και
και  Να βρεθεί το υπόλοιπο της διαίρεσης του πολυωνύμου
Να βρεθεί το υπόλοιπο της διαίρεσης του πολυωνύμου  Θεωρείστε ότι τα
Θεωρείστε ότι τα  δεν έχουν κοινούς παράγοντες ούτε το ένα είναι πολλαπλάσιο του άλλου,(είναι πρώτα μεταξύ τους)
δεν έχουν κοινούς παράγοντες ούτε το ένα είναι πολλαπλάσιο του άλλου,(είναι πρώτα μεταξύ τους)
![A(x),B(x) \in\mathbb{Z}[x] A(x),B(x) \in\mathbb{Z}[x]](/forum/ext/geomar/texintegr/latexrender/pictures/f6c76c52ebdd6cc1a9a68505b10e0ae3.png)
 δηλαδή
δηλαδή  . Όμως
. Όμως  άρα
άρα έχουμε είτε [
έχουμε είτε [  και
και  ] είτε [
] είτε [ 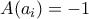 και
και  ].
].  , και φυσικά από την άλλη το πολυώνυμο
, και φυσικά από την άλλη το πολυώνυμο  είναι το πολύ
είναι το πολύ  βαθμού (αφού καθένα είναι τουλάχιστον πρώτου βαθμού).
βαθμού (αφού καθένα είναι τουλάχιστον πρώτου βαθμού).  και τότε
και τότε 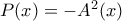 και από την υπόθεση
και από την υπόθεση 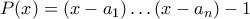 άρα τελικά
άρα τελικά  . Όμως εάν θέσουμε
. Όμως εάν θέσουμε 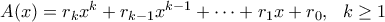 ,
, του
του 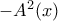 είναι το
είναι το  , ενώ του
, ενώ του  είναι το
είναι το  , δηλαδή
, δηλαδή  , άτοπο. (ΟΚ, στην πραγματικότητα το
, άτοπο. (ΟΚ, στην πραγματικότητα το  είναι ίσο με
είναι ίσο με  πρέπει να είναι μονικά πολυώνυμα).
πρέπει να είναι μονικά πολυώνυμα). με τα
με τα  να έχουν βαθμούς
να έχουν βαθμούς 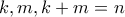 . Τότε
. Τότε  . Αυτό σημαίνει ότι κάθε
. Αυτό σημαίνει ότι κάθε  και το
και το  .Χρειαζόμαστε n φορές να εμφανισθεί το -1 σε κάποιο πολυώνυμο και n φορές να εμφανιθεί το +1. Δεν γίνεται και τα δύο πολυώνυμα να γίνουν -1 λιγότερες φορές από τον βαθμό τους διότι τότε θα είχαμε εμφανίσεις του -1 λιγότερες από
.Χρειαζόμαστε n φορές να εμφανισθεί το -1 σε κάποιο πολυώνυμο και n φορές να εμφανιθεί το +1. Δεν γίνεται και τα δύο πολυώνυμα να γίνουν -1 λιγότερες φορές από τον βαθμό τους διότι τότε θα είχαμε εμφανίσεις του -1 λιγότερες από  . Αν κάποιο όμως γίνει -1 περισσότερες φορές από τον βαθμό του θα είναι σταθερό. Συνεπώς κάθε ένα από τα δύο πολυώνυμα θα πρέπει να πάρει την τιμή -1 τόσες φορές όσες ο βαθμός του. Φυσικά το ίδιο επιχείρημα ισχύει και για το 1. 'Αρα τα πολυώνυμα
. Αν κάποιο όμως γίνει -1 περισσότερες φορές από τον βαθμό του θα είναι σταθερό. Συνεπώς κάθε ένα από τα δύο πολυώνυμα θα πρέπει να πάρει την τιμή -1 τόσες φορές όσες ο βαθμός του. Φυσικά το ίδιο επιχείρημα ισχύει και για το 1. 'Αρα τα πολυώνυμα 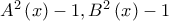 έχουν ρίζες όλους τους
έχουν ρίζες όλους τους  To το αυτό ισχύει με
To το αυτό ισχύει με  και το
και το  . καθώς και το
. καθώς και το  άρα και το
άρα και το  (άτοπο)
(άτοπο) ή
ή  ή
ή 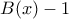 ή
ή  έχει περισσότερες ρίζες απ' ότι ο αντίστοιχος βαθμός του (όχι ν διαφορετικές ρίζες), άρα λοιπόν κάποιο από αυτά είναι το μηδενικό πολυώνυμο συνεπώς κάποιο από τα
έχει περισσότερες ρίζες απ' ότι ο αντίστοιχος βαθμός του (όχι ν διαφορετικές ρίζες), άρα λοιπόν κάποιο από αυτά είναι το μηδενικό πολυώνυμο συνεπώς κάποιο από τα 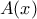 ή
ή  είναι μηδενικού βαθμού άτοπο.
είναι μηδενικού βαθμού άτοπο. .
. οπότε το
οπότε το  διαιρεί το
διαιρεί το  .
. .
. , και
, και  έπεται ότι
έπεται ότι  είναι βαθμού το πολύ
είναι βαθμού το πολύ  ,
, 
 .
.  είναι
είναι 

