Νομίζω ότι η παρακάτω άσκηση είναι ένα καλό ξεκίνημα για αυτόν τον φάκελο
Έστω
 πολυώνυμο με ακέραιους συντελεστές ώστε οι αριθμοί
πολυώνυμο με ακέραιους συντελεστές ώστε οι αριθμοί  και
και  να είναι και οι δυο περιττοί
να είναι και οι δυο περιττοίΔείξτε ότι το πολυώνυμο δεν μπορεί να έχει ακέραια ρίζα
Συντονιστής: exdx
 πολυώνυμο με ακέραιους συντελεστές ώστε οι αριθμοί
πολυώνυμο με ακέραιους συντελεστές ώστε οι αριθμοί  και
και  να είναι και οι δυο περιττοί
να είναι και οι δυο περιττοίΚαλωσόρισμα στον Ροδόλφο, σημαίνον πρόσωπο στα μαθηματικά δρώμενα του τόπου.R BORIS έγραψε:Συγχαρητήρια για την προσπάθεια
Νομίζω ότι η παρακάτω άσκηση είναι ένα καλό ξεκίνημα για αυτόν τον φάκελο
Έστωπολυώνυμο με ακέραιους συντελεστές ώστε οι αριθμοί
και
να είναι και οι δυο περιττοί
Δείξτε ότι το πολυώνυμο δεν μπορεί να έχει ακέραια ρίζα
 έχει
έχει  και
και 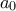 περιττούς. Για x άρτιο είναι
περιττούς. Για x άρτιο είναι 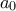 = περιττός άρα μη μηδενικός.
= περιττός άρα μη μηδενικός.
 = 1 (mod2) άρα μη μηδενικός.
= 1 (mod2) άρα μη μηδενικός.
 είναι μία ακέραια ρίζα του. Θα είναι
είναι μία ακέραια ρίζα του. Θα είναι 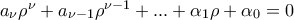 (1)
(1) =περιττός (2)
=περιττός (2) έχουμε ότι
έχουμε ότι  επί κάποιο ακέραιο
επί κάποιο ακέραιο 
 ως διαιρέτης περιττού είναι. Συνεπώς ο
ως διαιρέτης περιττού είναι. Συνεπώς ο  είναι άρτιος. Το άτοπο προκύπτει από την (1). Στο α' μέλος ο
είναι άρτιος. Το άτοπο προκύπτει από την (1). Στο α' μέλος ο  είναι άρτιος και ο
είναι άρτιος και ο 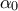 είναι περιττός. Το άθροισμα τους είναι ο άρτιος 0.
είναι περιττός. Το άθροισμα τους είναι ο άρτιος 0.Και να ήσαν μόνο οι εξαγωγές; Έχω επιφυλάξεις και για τις εισαγωγές.nsmavrogiannis έγραψε: Έννοια που εισήγαγε ο Gauss και εξήγαγαν...οι άνθρωποι του Παιδαγωγικού Ινστιτούτου.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες