Επιπλέον, θέλω να προτείνετε βιβλία τοπολογίας και όσο αφορά πιο πολύ τα κεφάλαια Συνεχείς Χώροι(δηλαδή αυτοί που είναι συμπαγείς, συνεκτικοί και Hausdorff), Τοπικά συνεκτικοί Χώροι, Συνεχή του Peano, Σημεία Τομής και να έχουν ασκήσεις μέσα στις οποίες να συμβουλευτώ.
- Έστω
 μετρικό συνεχές τέτοιο ώστε για κάθε δύο σημεία
μετρικό συνεχές τέτοιο ώστε για κάθε δύο σημεία 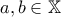 το σύνολο
το σύνολο  είναι μη συνεκτικό. Να δείξετε ότι το
είναι μη συνεκτικό. Να δείξετε ότι το  δεν έχει σημεία τομής.
δεν έχει σημεία τομής.
- Ένα συνεχές
 λέγεται αποσυνθέσιμο αν και μόνο αν είναι η ένωση δύο γνήσιων υποσυνεχών του, δηλαδή
λέγεται αποσυνθέσιμο αν και μόνο αν είναι η ένωση δύο γνήσιων υποσυνεχών του, δηλαδή 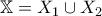 , όπου
, όπου  συνεχή διαφορετικά από το
συνεχή διαφορετικά από το  (Αν το
(Αν το  δεν είναι αποσυνθέσιμο τότε λέμε ότι το
δεν είναι αποσυνθέσιμο τότε λέμε ότι το  είναι αντιποσυνθέσιμο). Να δείξετε ότι:
είναι αντιποσυνθέσιμο). Να δείξετε ότι:
- Ένα συνεχές
 είναι αποσυνθέσιμο αν και μόνο αν το
είναι αποσυνθέσιμο αν και μόνο αν το  περιέχει ένα γνήσιο υποσυνεχές του οποίου το εσωτερικό είναι μη κενό.
περιέχει ένα γνήσιο υποσυνεχές του οποίου το εσωτερικό είναι μη κενό.
- Κάθε συνεχές του
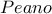 είναι αποσυνθέσιμο.
είναι αποσυνθέσιμο.
- Ένα συνεχές
- Έστω
 συμπαγής μετρικός χώρος. Να δείξετε ότι: Ο
συμπαγής μετρικός χώρος. Να δείξετε ότι: Ο  είναι τοπικά συνεκτικός αν και μόνο αν
είναι τοπικά συνεκτικός αν και μόνο αν  ,
, 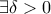 , τέτοιο ώστε για κάθε δύο σημεία
, τέτοιο ώστε για κάθε δύο σημεία 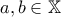 με
με 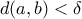 να υπάρχει υποσυνεχές
να υπάρχει υποσυνεχές  του
του  με
με 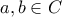 και
και  .
.

 του
του  είναι μη συνεκτικός.
είναι μη συνεκτικός.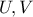 του
του 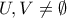 και
και 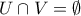 ώστε
ώστε  . Επιπλέον ισχύει ότι το
. Επιπλέον ισχύει ότι το  είναι ανοιχτό.
είναι ανοιχτό.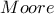 , ας είναι
, ας είναι 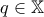 το σημείο μη τομής του
το σημείο μη τομής του 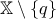 είναι συνεκτικός.
είναι συνεκτικός.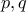 του
του 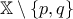 είναι μη συνεκτικός, εξ' υποθέσεως.
είναι μη συνεκτικός, εξ' υποθέσεως.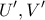 του
του 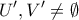 και
και 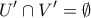 ώστε
ώστε 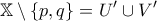 .
. .
.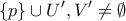 ,
, και
και 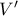 είναι ανοιχτά και
είναι ανοιχτά και  .
. χώρου
χώρου 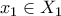 και κάθε
και κάθε  έχουμε ότι υπάρχουν τα ανοιχτά
έχουμε ότι υπάρχουν τα ανοιχτά 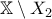 ,
, 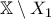 ώστε
ώστε 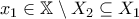 και
και  .
.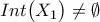 και
και  .
. του
του  με
με 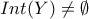 .
.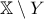 είναι συνεκτικό, τότε
είναι συνεκτικό, τότε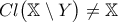 είναι:
είναι: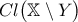 είναι γνήσιο υποσυνεχές του
είναι γνήσιο υποσυνεχές του  .
. είναι μη συνεκτικό, τότε
είναι μη συνεκτικό, τότε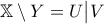 .
. ,
, 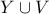 είναι υποσυνεχή του
είναι υποσυνεχή του  .
. και για κάθε ανοιχτή περιοχή
και για κάθε ανοιχτή περιοχή  του
του  στον
στον  του
του  .
.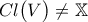 είναι:
είναι: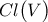 είναι γνήσιο υποσυνεχές του
είναι γνήσιο υποσυνεχές του 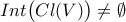 , αφού
, αφού  .
.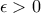 :
: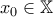 , έχουμε την ανοιχτή περιοχή
, έχουμε την ανοιχτή περιοχή 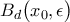 .
.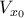 του
του  στον
στον 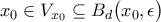 .
. ,
,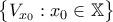 είναι ανοιχτή κάλυψη του
είναι ανοιχτή κάλυψη του 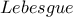 για κάθε ανοιχτή κάλυψή του.
για κάθε ανοιχτή κάλυψή του.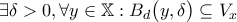 .
.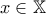 μπορούμε να επιλέξουμε
μπορούμε να επιλέξουμε  ώστε
ώστε 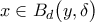 και αυτό επιτυχγάνεται διότι επιλέγουμε οποιοδήποτε
και αυτό επιτυχγάνεται διότι επιλέγουμε οποιοδήποτε  .
.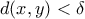 και
και 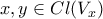 .
.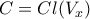 είναι:
είναι: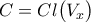 είναι υποσυνεχές του
είναι υποσυνεχές του  .
.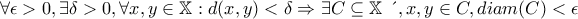 .
. .
.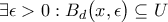 , όπου
, όπου 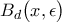 είναι ανοιχτό(το οποίο υπάρχει διότι μια βάση του τοπολολγικού χώρου μας είναι η συλλογή όλων αυτών των ανοιχτών μπαλών) και συνεκτικό(καθώς έχουμε αποδείξει ότι είναι δρομοσυνεκτικός) που περιχέχει το
είναι ανοιχτό(το οποίο υπάρχει διότι μια βάση του τοπολολγικού χώρου μας είναι η συλλογή όλων αυτών των ανοιχτών μπαλών) και συνεκτικό(καθώς έχουμε αποδείξει ότι είναι δρομοσυνεκτικός) που περιχέχει το