 ένας σταθερός, αντιστρέψιμος,
ένας σταθερός, αντιστρέψιμος,  πίνακας του δ.χ.
πίνακας του δ.χ.  . Να βρεθεί η διάσταση και μια βάση του υποχώρου
. Να βρεθεί η διάσταση και μια βάση του υποχώρου 
Έως και 8/2/2021
Συντονιστής: Demetres
 ένας σταθερός, αντιστρέψιμος,
ένας σταθερός, αντιστρέψιμος,  πίνακας του δ.χ.
πίνακας του δ.χ.  . Να βρεθεί η διάσταση και μια βάση του υποχώρου
. Να βρεθεί η διάσταση και μια βάση του υποχώρου 

 ο υπόχωρος του
ο υπόχωρος του  που περιέχει όλους τους διαγώνιους πίνακες
που περιέχει όλους τους διαγώνιους πίνακες  .
. προκύπτει από τον υπόχωρο
προκύπτει από τον υπόχωρο  με το μετασχηματισμό
με το μετασχηματισμό  .
. προκύπτει από το
προκύπτει από το  με το μετασχηματισμό
με το μετασχηματισμό  .
. είναι ισόμορφοι.
είναι ισόμορφοι.  και μια βάση η
και μια βάση η  , όπου
, όπου  μια βάση του
μια βάση του  .
.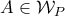 υπάρχει διαγώνιος πίνακας
υπάρχει διαγώνιος πίνακας  τέτοιος ώστε
τέτοιος ώστε 

 παράγουν τον υπόχωρο
παράγουν τον υπόχωρο  και επειδή είναι γραμμικώς ανεξάρτητα στοιχεία του
και επειδή είναι γραμμικώς ανεξάρτητα στοιχεία του  , έπεται ότι αποτελούν μια βάση του. Άρα
, έπεται ότι αποτελούν μια βάση του. Άρα  .
.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες