Όριο ολοκληρωμάτων
Δημοσιεύτηκε: Παρ Φεβ 15, 2019 6:51 pm
Έστω η συνεχής συνάρτηση ![f:\left [ -1,1 \right ]\longrightarrow \mathbb{R} f:\left [ -1,1 \right ]\longrightarrow \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/c97ca4e73be2155a08e99de9092bd68e.png) . Να αποδείξετε ότι:
. Να αποδείξετε ότι:
 Φιλικά,
Φιλικά,
Μάριος
Μέχρι 17/02/2019.
![f:\left [ -1,1 \right ]\longrightarrow \mathbb{R} f:\left [ -1,1 \right ]\longrightarrow \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/c97ca4e73be2155a08e99de9092bd68e.png) . Να αποδείξετε ότι:
. Να αποδείξετε ότι: Φιλικά,
Φιλικά,Μάριος
Μέχρι 17/02/2019.
![f:\left [ -1,1 \right ]\longrightarrow \mathbb{R} f:\left [ -1,1 \right ]\longrightarrow \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/c97ca4e73be2155a08e99de9092bd68e.png) . Να αποδείξετε ότι:
. Να αποδείξετε ότι: Φιλικά,
Φιλικά,Βάζω μια λύση παρακάτω με κάποια επιφύλαξη για τυχόν λογιστικό σφάλμα, έστω:

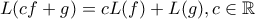 , προκύπτει απλά με πράξεις, και:
, προκύπτει απλά με πράξεις, και:
 , αν l περιττός άμεσα το όριο μηδέν αφού η συνάρτηση εντός του ολοκληρώματος του αριθμητή είναι περιττή,και το ολοκλήρωμα είναι σε συμμετρικό γύρω από το 0 διάστημα.
, αν l περιττός άμεσα το όριο μηδέν αφού η συνάρτηση εντός του ολοκληρώματος του αριθμητή είναι περιττή,και το ολοκλήρωμα είναι σε συμμετρικό γύρω από το 0 διάστημα.



![[-1,1] [-1,1]](/forum/ext/geomar/texintegr/latexrender/pictures/d060b17b29e0dae91a1cac23ea62281a.png) άρα για το δοθέν ε υπάρχει πολυώνυμο έτσι ώστε:
άρα για το δοθέν ε υπάρχει πολυώνυμο έτσι ώστε: (Weierstrass)
(Weierstrass)
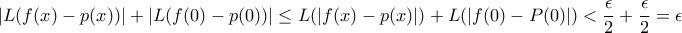
Στην σχέσηsot arm έγραψε: ↑Κυρ Φεβ 17, 2019 2:55 pmΒάζω μια λύση παρακάτω με κάποια επιφύλαξη για τυχόν λογιστικό σφάλμα, έστω:
Παρατηρώ ότι είναι γραμμική, πράγματι:
, προκύπτει απλά με πράξεις, και:
Εξετάζουμε τώρα μονώνυμα της μορφής, αν l περιττός άμεσα το όριο μηδέν αφού η συνάρτηση εντός του ολοκληρώματος του αριθμητή είναι περιττή,και το ολοκλήρωμα είναι σε συμμετρικό γύρω από το 0 διάστημα.
Αν πάλι l άρτιος προκύπτει με παραγοντική:
Ο παρονομαστής είναι εφαρμογή του παραπάνω για κ=0, έχω λοιπόν για το κλάσμα:
Από τα παραπάνω για κάθε πολυώνυμο έχω:
αφού όλες οι δυνάμεις του x δίνουν μηδέν και ο σταθερός όρος ισούται με
Έστω ε>0 τυχόν, η f είναι συνεχής στοάρα για το δοθέν ε υπάρχει πολυώνυμο έτσι ώστε:
(Weierstrass)
Άρα:
και τελειώσαμε, ξαναλέω με κάποια επιφύλαξη για λογιστικό σφάλμα, αλλά νομίζω η ιδέα είναι η σωστή.


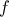 παντού είναι περιττή.
παντού είναι περιττή.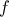 είναι συνεχής στο
είναι συνεχής στο  και έχουμε ακόμα μια συνθήκη.
και έχουμε ακόμα μια συνθήκη.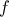 φραγμένη η
φραγμένη η  υπάρχει.
υπάρχει.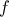 συνεχής για
συνεχής για 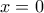 και φραγμένη.
και φραγμένη. (1)
(1)![A_\delta =[-1,1]\setminus [-\delta ,\delta ] A_\delta =[-1,1]\setminus [-\delta ,\delta ]](/forum/ext/geomar/texintegr/latexrender/pictures/e99051cd59b7c9ba4bfc42e26d063895.png) για
για 



![\exists M>0\forall x\in[-1,1]:|f(x)|\leq M \exists M>0\forall x\in[-1,1]:|f(x)|\leq M](/forum/ext/geomar/texintegr/latexrender/pictures/aa13681f1fbf4c0d77641b489e76b40e.png)





![f:[-1,1]\rightarrow \mathbb{R} f:[-1,1]\rightarrow \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/105fdf393ff64f4184d3ad75d0f61e51.png)
 και ολοκληρώσιμη
και ολοκληρώσιμη 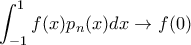







 είναι
είναι 

 έχουμε αν ονομάσουμε
έχουμε αν ονομάσουμε



 του Dirac.
του Dirac.