Ας ξεκουραστούμε.

Φανης Θεοφανιδης · #1

: 105.png (15.42 KiB) Προβλήθηκε 593 φορές

Καλησπέρα.

Τα χρωματιστά τρίγωνα του σχήματος, είναι ισόπλευρα.
Αν $N\equiv AD\cap EC$ , να δείξετε ότι τα σημεία B, D, N, E

είναι ομοκυκλικά.

cool geometry · #2

έστω $AB=a, BD=k\cdot a$
στο $\bigtriangleup ABD:AB=a,BD=k\cdot a,\angle ABD=60^{0}\Rightarrow AD^{2}=a^{2}+a^{2}k^{2}-a\cdot k\cdot a=a^{2}(k^{2}-k+1)\Rightarrow \frac{a^{2}(k^{2}-k+1)}{\frac{3}{4}}=\frac{a^{2}\cdot k^{2}}{cos^{2}\angle BAD}\Rightarrow cos^{2}\angle BAD=\frac{3k^{2}}{4(k^{2}-k+1)}(1)$
στο $\bigtriangleup DCE:DE=k\cdot a, DC=(1-k)\cdot a,\angle EDC=120^{0}\Rightarrow EC^{2}=k^{2}a^{2}+(1-k)^{2}a^{2}+k(1-k)a^{2}=(k^{2}-k+1)a^{2}\Rightarrow \frac{a^{2}(k^{2}-k+1)}{\frac{3}{4}}=\frac{a^{2}k^{2}}{cos^{2}\angle DCE}\Rightarrow cos^{2}\angle DCE=\frac{3k^{2}}{4(k^{2}-k+1)}(2)$
Οι δύο αυτές σχέσεις μας οδηγούν στην ισότητα γωνιών $\angle BAN=\angle BCN\Rightarrow ABNC$ εγγράψιμο και τώρα είναι:
$\angle BNE=\angle BAC=60^{0}=\angle BDE\Rightarrow BDNE$ εγγράψιμο και το ζητούμενο έχει αποδειχθεί.

cool geometry · #3

και μία απλούστερη λύση...
είναι $AB=BC,BE=BD,\angle ABD=\angle CBE,$ άρα $\bigtriangleup ABD=\bigtriangleup BCE$ και κατά συνέπεια θα ισχύει $\angle BCE=\angle BAD\Rightarrow \angle BCN=\angle BAN\Rightarrow ABNC$ εγγράψιμο με άμεση συνέπεια $\angle BNE=\angle BAC=\angle BDE\Rightarrow BDNE$ εγγράψιμο και το ζητούμενο έχει αποδειχθεί.

#4

Φανης Θεοφανιδης έγραψε: ↑
Παρ Αύγ 12, 2022 8:01 pm
105.png

Καλησπέρα.

Τα χρωματιστά τρίγωνα του σχήματος, είναι ισόπλευρα.
Αν $N\equiv AD\cap EC$ , να δείξετε ότι τα σημεία είναι ομοκυκλικά.

Στο σχήμα του Φάνη.

Εύκολα διαπιστώνουμε ότι $\vartriangle ABD=\vartriangle CBE\left( AB=CB,BD=BE,\angle ABD=\angle CBE={{60}^{0}} \right)$ $\Rightarrow \angle BAN\equiv \angle ABD=\angle BCE\equiv \angle BCN\Rightarrow A,B,N,C$ ομοκυκλικά ,

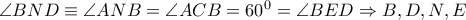άρα $\angle BND\equiv \angle ANB=\angle ACB={{60}^{0}}=\angle BED\Rightarrow B,D,N,E$ ομοκυκλικά και το ζητούμενο έχει αποδειχθεί.

Υ.Σ. Ο Φάνης είπε να ξεκουραστούμε

#5

Φανης Θεοφανιδης έγραψε: ↑
Παρ Αύγ 12, 2022 8:01 pm
105.png

Καλησπέρα.

Τα χρωματιστά τρίγωνα του σχήματος, είναι ισόπλευρα.
Αν $N\equiv AD\cap EC$ , να δείξετε ότι τα σημεία είναι ομοκυκλικά.

Προεκτείνω την

μέχρι να κόψει στο

την

. Είναι:

1. το τετράπλευρο ABET

παραλληλόγραμμο .

2. Το $\vartriangle TDC$ ισόπλευρο

3. Το τετράπλευρο TBEC

ισοσκελές τραπέζιο γιατί έχει ίσες διαγώνιους.

4. Το τετράπλευρο ABTD

ισοσκελές τραπέζιο .( προφανές)

: Ας ξεκουραστούμε.png (27.68 KiB) Προβλήθηκε 515 φορές

Έτσι θα έχω $\widehat {{\theta _1}} = \widehat {{\theta _2}} = \widehat {{\theta _3}}$ , οπότε τα τρίγωνα $TAD\,\,\kappa \alpha \iota \,\,NED$ είναι ισογώνια ,

συνεπώς $\widehat {{\omega _{}}} = 120^\circ$ και το τετράπλευρο BEND

έχει τις γωνίες του στα $B\,\,\kappa \alpha \iota \,\,N$ παραπληρωματικές , δηλαδή είναι εγγράψιμο .

#6

Ας το δούμε κι αλλιώς:

Έστω N_1

το δεύτερο σημείο τομής των κύκλων ABC

και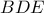

. Φορσέ οι τρεις διαδοχικές οξείες γωνίες με κορυφή το N_1

είναι

, οπότε τα E, N_1,C

είναι συνευθειακά, άρα τα N, N_1

συμπίπτουν κ.λπ.

Μιχάλης Τσουρακάκης · #7

Φανης Θεοφανιδης έγραψε: ↑
Παρ Αύγ 12, 2022 8:01 pm
105.png

Καλησπέρα.

Τα χρωματιστά τρίγωνα του σχήματος, είναι ισόπλευρα.
Αν $N\equiv AD\cap EC$ , να δείξετε ότι τα σημεία είναι ομοκυκλικά.

Με

συμμετρικό του

ως προς

,προφανώς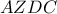

ισοσκελές τραπέζιο ,συνεπώς οι γωνίες $\omega$ είναι ίσες και το ABNC

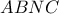εγγράψιμμο

Άρα $\angle ANC=60^0= \angle DBE \Rightarrow B, D, N ,E$ ομοκυκλικά

: ομοκυκλικά.png (219.65 KiB) Προβλήθηκε 438 φορές

Ας ξεκουραστούμε.

Ας ξεκουραστούμε.

Re: Ας ξεκουραστούμε.

Re: Ας ξεκουραστούμε.

Re: Ας ξεκουραστούμε.

Re: Ας ξεκουραστούμε.

Re: Ας ξεκουραστούμε.

Re: Ας ξεκουραστούμε.

Μέλη σε σύνδεση