 είναι τα ύψη οξυγώνιου τριγώνου
είναι τα ύψη οξυγώνιου τριγώνου  και
και  είναι ένα από τα σημεία τομής της
είναι ένα από τα σημεία τομής της με τον περίκυκλο του τριγώνου. Αν οι
με τον περίκυκλο του τριγώνου. Αν οι  τένμνονται στο
τένμνονται στο  να δείξετε ότι
να δείξετε ότι 
Ας την αφήσουμε 24 ώρες για μαθητές.
Συντονιστής: Μιχάλης Νάννος
 είναι τα ύψη οξυγώνιου τριγώνου
είναι τα ύψη οξυγώνιου τριγώνου  και
και  είναι ένα από τα σημεία τομής της
είναι ένα από τα σημεία τομής της με τον περίκυκλο του τριγώνου. Αν οι
με τον περίκυκλο του τριγώνου. Αν οι  τένμνονται στο
τένμνονται στο  να δείξετε ότι
να δείξετε ότι 
 είναι εγγεγραμμένο στον περίκυκλο του τριγώνου
είναι εγγεγραμμένο στον περίκυκλο του τριγώνου  . Επομένως, ισχύει:
. Επομένως, ισχύει:  .
.  το ορθόκεντρο του τριγώνου
το ορθόκεντρο του τριγώνου  . Τότε, το τετράπλευρο
. Τότε, το τετράπλευρο  είναι εγγράψιμο, άρα:
είναι εγγράψιμο, άρα:  .
.  είναι εγγράψιμο. Συνεπώς:
είναι εγγράψιμο. Συνεπώς:  .
.  . Όμως, προκύπτει
. Όμως, προκύπτει  και άρα το τετράπλευρο
και άρα το τετράπλευρο  είναι εγγράψιμο.
είναι εγγράψιμο.  είναι εγγράψιμο. Επομένως,
είναι εγγράψιμο. Επομένως,  . Από την εγγραψιμότητα του τετραπλεύρου
. Από την εγγραψιμότητα του τετραπλεύρου  προκύπτει:
προκύπτει: 
 , άρα το τρίγωνο
, άρα το τρίγωνο 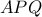 είναι ισοσκελές, οπότε:
είναι ισοσκελές, οπότε: 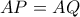
 .
. , έχουμε ότι
, έχουμε ότι  .
. , έχουμε ότι
, έχουμε ότι  .
. είναι εγγράψιμο, γιατί τότε θα ισχύει:
είναι εγγράψιμο, γιατί τότε θα ισχύει:  .
. , δηλαδή ότι
, δηλαδή ότι  .
. είναι το ορθόκεντρο του τριγώνου
είναι το ορθόκεντρο του τριγώνου  , από το εγγράψιμο τετράπλευρο
, από το εγγράψιμο τετράπλευρο  έχουμε ότι
έχουμε ότι  (ως οξείες γωνίες με κάθετες πλευρές) και το ζητούμενο δείχτηκε.
(ως οξείες γωνίες με κάθετες πλευρές) και το ζητούμενο δείχτηκε.Μια χαρά την αξιολόγησες. Κι όμως είναι από 2010 IMO Shortlist!ΦΙΛΙΠΠΟΣ ΚΑΛΟΥΔΗΣ έγραψε: ↑Πέμ Ιαν 20, 2022 2:58 pmΘεωρώ πως είναι για επίπεδο Αρχιμήδης junior- Ευκλείδης senior στην καλύτερη περίπτωση.
 εγγράψιμο , άρα
εγγράψιμο , άρα 
 εγγράψιμο, άρα
εγγράψιμο, άρα 
 , άρα
, άρα  ( από εγγράψιμο
( από εγγράψιμο  )
) που αποδεικνύει το ζητούμενο.
που αποδεικνύει το ζητούμενο.Μέλη σε αυτήν τη Δ. Συζήτηση: Bing [Bot] και 1 επισκέπτης