Λόγω συμμετρίας προκύπτει άμεσα ότι

, οπότε σύμφωνα με γνωστό λήμμα (βλέπε το λήμμα 1
viewtopic.php?f=22&t=68789&p=334622#p334622) ο περιγεγραμμένος
κύκλος
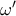
του

διέρχεται από το μέσο

του τόξου

του περιγεγραμμένου κύκλου

του

.
Έστω ότι η διχοτόµος της γωνίας

τέµνει τον κύκλο

του στο σηµείο

,
που είναι το µέσο του τόξου

που δεν περιέχει την κορυφή

, δηλαδή,

.
Εποµένως, το

είναι τετράπλευρο του οποίου οι διαγώνιοί του τέµνονται κάθετα στο σηµείο

,
που είναι το µέσο της

.

- paral_from_mid.png (35.89 KiB) Προβλήθηκε 739 φορές
΄Οµοια, το

είναι το µέσο του τόξου

του κύκλου
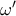
και το σηµείο
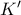
είναι το µέσο του

.
Εφόσον το

είναι ισοσκελές, και η γωνία της κορυφής του ισούται µε τη γωνία BAC, τότε

.
Τώρα, τα τρίγωνα

και

είναι όµοια, εφόσον

(χρησιµοποιείται δύο ϕορές το γεγονός ότι γωνίες εγγεγραµµένες στο ίδιο τόξο
είναι ίσες), και

. Από τα παραπάνω προκύπτει ότι
τα

και
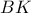
είναι ύψη των τριγώνων

και

αντίστοιχα. Εποµένως, τα σηµεία
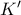
και

διαιρούν τις πλευρές

και

σε ίσους λόγους, δηλαδή, οι ευθείες

και

είναι παράλληλες, οπότε άµεσα προκύπτει το ζητούµενο.
 τα σημεία επαφής του έγκυκλου
τα σημεία επαφής του έγκυκλου  τριγώνου
τριγώνου  με τις πλευρές του
με τις πλευρές του  αντίστοιχα και ας είναι
αντίστοιχα και ας είναι  τα συμμετρικά των
τα συμμετρικά των  ως προς τα μέσα
ως προς τα μέσα 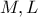 των
των  αντίστοιχα (δεν τα ονομάζω ισοτομικά για να δικαιολογείται ο φάκελος
αντίστοιχα (δεν τα ονομάζω ισοτομικά για να δικαιολογείται ο φάκελος  , όπου
, όπου  τα μέσα των
τα μέσα των  αντίστοιχα και
αντίστοιχα και  το κέντρο του έγκυκλου.
το κέντρο του έγκυκλου. 
 Δηλαδή τα τετράπλευρα
Δηλαδή τα τετράπλευρα 

 δηλαδή το τριγωνο
δηλαδή το τριγωνο  είναι ισοσκελές και
είναι ισοσκελές και  ,γιατί εχουν πλευρές παράλληλες και στο παραλληλόγραμμο
,γιατί εχουν πλευρές παράλληλες και στο παραλληλόγραμμο 
 ,η
,η  Ειναι και διχοτόμος της γωνίας
Ειναι και διχοτόμος της γωνίας  οπότε τα τρίγωνα
οπότε τα τρίγωνα  είναι ίσα και οι διχοτόμοι των ίσων γωνιών παραλληλες
είναι ίσα και οι διχοτόμοι των ίσων γωνιών παραλληλες το συμμετρικό του
το συμμετρικό του  ως προς το
ως προς το  . Τότε
. Τότε  (ως συνδέουσα τα μέσα δύο πλευρών τριγώνου) και
(ως συνδέουσα τα μέσα δύο πλευρών τριγώνου) και  παραλληλόγραμμο (οι διαγώνιές του διχοτομούνται), οπότε:
παραλληλόγραμμο (οι διαγώνιές του διχοτομούνται), οπότε:  και συνεπώς το τρίγωνο
και συνεπώς το τρίγωνο  είναι ισοσκελές, άρα
είναι ισοσκελές, άρα 
 φέρνω τις
φέρνω τις  παράλληλες στην
παράλληλες στην  και επειδή η
και επειδή η  θα
θα  Τα τρίγωνα, λοιπόν,
Τα τρίγωνα, λοιπόν,  έχουν δύο πλευρές ίσες μία προς μία και
έχουν δύο πλευρές ίσες μία προς μία και  άρα
άρα  Αλλά,
Αλλά,  και
και  είμαι στη διάθεσή του).
είμαι στη διάθεσή του). , οπότε σύμφωνα με γνωστό λήμμα (βλέπε το λήμμα 1
, οπότε σύμφωνα με γνωστό λήμμα (βλέπε το λήμμα 1 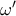 του
του  διέρχεται από το μέσο
διέρχεται από το μέσο  του τόξου
του τόξου  του περιγεγραμμένου κύκλου
του περιγεγραμμένου κύκλου 
 .
. ,
,  που δεν περιέχει την κορυφή
που δεν περιέχει την κορυφή  , δηλαδή,
, δηλαδή,  .
.  είναι τετράπλευρο του οποίου οι διαγώνιοί του τέµνονται κάθετα στο σηµείο
είναι τετράπλευρο του οποίου οι διαγώνιοί του τέµνονται κάθετα στο σηµείο  είναι το µέσο του τόξου
είναι το µέσο του τόξου  του κύκλου
του κύκλου 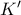 είναι το µέσο του
είναι το µέσο του  είναι ισοσκελές, και η γωνία της κορυφής του ισούται µε τη γωνία BAC, τότε
είναι ισοσκελές, και η γωνία της κορυφής του ισούται µε τη γωνία BAC, τότε  .
. και
και  είναι όµοια, εφόσον
είναι όµοια, εφόσον 
 . Από τα παραπάνω προκύπτει ότι
. Από τα παραπάνω προκύπτει ότι και
και 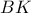 είναι ύψη των τριγώνων
είναι ύψη των τριγώνων  και
και  σε ίσους λόγους, δηλαδή, οι ευθείες
σε ίσους λόγους, δηλαδή, οι ευθείες  και
και  έχουν
έχουν  και
και  Θα δείξω ότι
Θα δείξω ότι 
 η πρόταση προφανώς ισχύει. Χωρίς βλάβη υποθέτω ότι η
η πρόταση προφανώς ισχύει. Χωρίς βλάβη υποθέτω ότι η  είναι οξεία και η
είναι οξεία και η  αμβλεία. Στην
αμβλεία. Στην  προς το
προς το  θεωρώ σημείο
θεωρώ σημείο  ώστε
ώστε  Τα αμβλυγώνια τρίγωνα
Τα αμβλυγώνια τρίγωνα  έχουν
έχουν ίσες και
ίσες και  άρα είναι ίσα (έμμεσο κριτήριο ισότητας). Οπότε
άρα είναι ίσα (έμμεσο κριτήριο ισότητας). Οπότε  Αλλά το
Αλλά το  είναι ισοσκελές και
είναι ισοσκελές και  άρα
άρα  και το ζητούμενο αποδείχτηκε.
και το ζητούμενο αποδείχτηκε. ως προς το
ως προς το  άρα αρκεί να αποδείξουμε ότι:
άρα αρκεί να αποδείξουμε ότι: . Λοιπόν έχουμε και λέμε:
. Λοιπόν έχουμε και λέμε: όμως λόγω
όμως λόγω  θα είναι
θα είναι  και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί.