
Γνωστή και μη εξαιρετέα
Συντονιστής: Μιχάλης Νάννος
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13278
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Γνωστή και μη εξαιρετέα
Πιθανόν να έχει τεθεί ξανά (με τόσες που κυκλοφορούν έχω χάσει το λογαριασμό).
Να βρείτε τη γωνία 

Λέξεις Κλειδιά:
-
Φανης Θεοφανιδης
- Δημοσιεύσεις: 1419
- Εγγραφή: Παρ Απρ 10, 2015 9:04 pm
Re: Γνωστή και μη εξαιρετέα
Καλημέρα.
Γράφω τον περίκυκλο του
 του οποίου το κέντρο ονομάζω
του οποίου το κέντρο ονομάζω  .
.Οι κόκκινες γωνίες προκύπτουν εύκολα.
Λήμμα: Είναι
 (Η απόδειξη αργότερα).
(Η απόδειξη αργότερα).Άρα το
 είναι εγγράψιμο.
είναι εγγράψιμο.Επομένως
 .
.Συνεπώς
 .
.-
Φανης Θεοφανιδης
- Δημοσιεύσεις: 1419
- Εγγραφή: Παρ Απρ 10, 2015 9:04 pm
Re: Γνωστή και μη εξαιρετέα
Απομονώνω το τρίγωνο
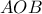 μαζί με τα στοιχεία που έχουν προκύψει από το παραπάνω σχήμα.
μαζί με τα στοιχεία που έχουν προκύψει από το παραπάνω σχήμα.Γράφω τον περίκυκλο του
 του οποίου το κέντρο ονομάζω
του οποίου το κέντρο ονομάζω  και
και  το σημείο
το σημείοτομής του με την
 . Φέρνω όλα τα κόκκινα τμήματα. Προφανώς το
. Φέρνω όλα τα κόκκινα τμήματα. Προφανώς το  είναι ισόπλευρο.
είναι ισόπλευρο.Οπότε
 . Επίσης
. Επίσης  (αφού το
(αφού το  είναι εγγράψιμο)
είναι εγγράψιμο)
 . Αλλά η
. Αλλά η  είναι μεσοκάθετος του
είναι μεσοκάθετος του  . Άρα
. Άρα  .
.Από το άθροισμα των γωνιών του
 έπεται ότι
έπεται ότι  .
.Επομένως
 .
.Συνεπώς
 . Δηλαδή
. Δηλαδή  .
.Re: Γνωστή και μη εξαιρετέα
Δείτε το σχήμα
Τα τρίγωνα είναι ίσα και ισοσκελή τύπου
είναι ίσα και ισοσκελή τύπου  και όμοια με το αρχικό ,
και όμοια με το αρχικό ,  .
.
Το τραπέζιο είναι υπέρ ισοσκελές και
είναι υπέρ ισοσκελές και  .
.
Αναλυτικά
Έστω το σημείο τομής των
το σημείο τομής των  . Το
. Το  δηλαδή είναι ισογώνιο με το
δηλαδή είναι ισογώνιο με το 
Φέρνω και τη διάμεσο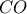 του
του  που είναι ύψος και διχοτόμος άρα
που είναι ύψος και διχοτόμος άρα  .
.
Η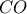 τέμνει τις
τέμνει τις  στα
στα 
ενώ η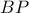
 στο
στο  θα είναι
θα είναι 
Το θα είναι το ορθόκεντρο του
θα είναι το ορθόκεντρο του  .
.
Τώρα φέρνω:
Το τρίτο ύψος και την
και την  που τέμνει το
που τέμνει το  στο
στο  και την
και την  στο
στο  .
.
Το είναι προφανώς ίσο με το
είναι προφανώς ίσο με το 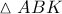 και αβίαστα προκύπτουν οι γωνίες που σημειώνονται στο σχήμα.
και αβίαστα προκύπτουν οι γωνίες που σημειώνονται στο σχήμα.
Η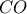 είναι άξονας συμμετρίας του
είναι άξονας συμμετρίας του  και του χαρταετού
και του χαρταετού  .
.
Το τετράπλευρο είναι ισοσκελές τραπέζιο και μάλιστα :
είναι ισοσκελές τραπέζιο και μάλιστα :  .
.
Αν το σημείο τομής των διαγώνιων του χαρταετού
το σημείο τομής των διαγώνιων του χαρταετού  θα έχω :
θα έχω :
 ,
,
σχέση που μας εξασφαλίζει ότι


Τα τρίγωνα
 είναι ίσα και ισοσκελή τύπου
είναι ίσα και ισοσκελή τύπου  και όμοια με το αρχικό ,
και όμοια με το αρχικό ,  .
.Το τραπέζιο
 είναι υπέρ ισοσκελές και
είναι υπέρ ισοσκελές και  .
.Αναλυτικά
Έστω
 το σημείο τομής των
το σημείο τομής των  . Το
. Το  δηλαδή είναι ισογώνιο με το
δηλαδή είναι ισογώνιο με το 
Φέρνω και τη διάμεσο
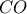 του
του  που είναι ύψος και διχοτόμος άρα
που είναι ύψος και διχοτόμος άρα  .
. Η
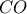 τέμνει τις
τέμνει τις  στα
στα 
ενώ η
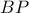
 στο
στο  θα είναι
θα είναι 
Το
 θα είναι το ορθόκεντρο του
θα είναι το ορθόκεντρο του  .
.Τώρα φέρνω:
Το τρίτο ύψος
 και την
και την  που τέμνει το
που τέμνει το  στο
στο  και την
και την  στο
στο  .
.Το
 είναι προφανώς ίσο με το
είναι προφανώς ίσο με το 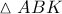 και αβίαστα προκύπτουν οι γωνίες που σημειώνονται στο σχήμα.
και αβίαστα προκύπτουν οι γωνίες που σημειώνονται στο σχήμα.Η
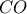 είναι άξονας συμμετρίας του
είναι άξονας συμμετρίας του  και του χαρταετού
και του χαρταετού  .
. Το τετράπλευρο
 είναι ισοσκελές τραπέζιο και μάλιστα :
είναι ισοσκελές τραπέζιο και μάλιστα :  .
.Αν
 το σημείο τομής των διαγώνιων του χαρταετού
το σημείο τομής των διαγώνιων του χαρταετού  θα έχω :
θα έχω : ,
, σχέση που μας εξασφαλίζει ότι


- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13278
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: Γνωστή και μη εξαιρετέα
Κατασκευάζω το ισόπλευρο  και έστω
και έστω  οι προβολές του
οι προβολές του  στις
στις  αντίστοιχα.
Επειδή η
αντίστοιχα.
Επειδή η  διχοτομεί τη γωνία
διχοτομεί τη γωνία 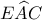 θα είναι
θα είναι  Εξάλλου,
Εξάλλου,  οπότε
οπότε 
και Άρα η
Άρα η 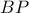 διχοτομεί την
διχοτομεί την  και
και  οπότε τα ορθογώνια τρίγωνα
οπότε τα ορθογώνια τρίγωνα
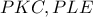 είναι ίσα και κατά συνέπεια
είναι ίσα και κατά συνέπεια  δηλαδή το
δηλαδή το  είναι εγγράψιμο, άρα
είναι εγγράψιμο, άρα 
Υπάρχει μία πολύ ωραία λύση με ύλη Β' λυκείου (δεν είναι δική μου). Αν θέλει μπορεί κάποιος να το προσπαθήσει.
 και έστω
και έστω  οι προβολές του
οι προβολές του  στις
στις  αντίστοιχα.
Επειδή η
αντίστοιχα.
Επειδή η  διχοτομεί τη γωνία
διχοτομεί τη γωνία 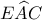 θα είναι
θα είναι  Εξάλλου,
Εξάλλου,  οπότε
οπότε 
και
 Άρα η
Άρα η 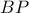 διχοτομεί την
διχοτομεί την  και
και  οπότε τα ορθογώνια τρίγωνα
οπότε τα ορθογώνια τρίγωνα 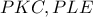 είναι ίσα και κατά συνέπεια
είναι ίσα και κατά συνέπεια  δηλαδή το
δηλαδή το  είναι εγγράψιμο, άρα
είναι εγγράψιμο, άρα 
Υπάρχει μία πολύ ωραία λύση με ύλη Β' λυκείου (δεν είναι δική μου). Αν θέλει μπορεί κάποιος να το προσπαθήσει.
-
cool geometry
- Δημοσιεύσεις: 292
- Εγγραφή: Τρί Αύγ 02, 2022 7:28 am
Re: Γνωστή και μη εξαιρετέα
Στο τρίγωνο  μπορούμε να αλλάξουμε τα ζεύγη και να υποθέσουμε ότι
μπορούμε να αλλάξουμε τα ζεύγη και να υποθέσουμε ότι  Τότε αρκεί να υπολογίσουμε τη γωνία
Τότε αρκεί να υπολογίσουμε τη γωνία  Λοιπόν κατασκευάζουμε το ισόπλευρο τρίγωνο
Λοιπόν κατασκευάζουμε το ισόπλευρο τρίγωνο  στο εξωτερικό του δοσμένου τριγώνου , τότε θα είναι
στο εξωτερικό του δοσμένου τριγώνου , τότε θα είναι  άρα το
άρα το  βρίσκεται πάνω στην
βρίσκεται πάνω στην  επομένως θα έχουμε
επομένως θα έχουμε  άρα το
άρα το  είναι περίκεντρο του τριγώνου
είναι περίκεντρο του τριγώνου  έτσι
έτσι 
 μπορούμε να αλλάξουμε τα ζεύγη και να υποθέσουμε ότι
μπορούμε να αλλάξουμε τα ζεύγη και να υποθέσουμε ότι  Τότε αρκεί να υπολογίσουμε τη γωνία
Τότε αρκεί να υπολογίσουμε τη γωνία  Λοιπόν κατασκευάζουμε το ισόπλευρο τρίγωνο
Λοιπόν κατασκευάζουμε το ισόπλευρο τρίγωνο  στο εξωτερικό του δοσμένου τριγώνου , τότε θα είναι
στο εξωτερικό του δοσμένου τριγώνου , τότε θα είναι  άρα το
άρα το  βρίσκεται πάνω στην
βρίσκεται πάνω στην  επομένως θα έχουμε
επομένως θα έχουμε  άρα το
άρα το  είναι περίκεντρο του τριγώνου
είναι περίκεντρο του τριγώνου  έτσι
έτσι 
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες
