Εφαπτόμενοι κύκλοι 1.
Δημοσιεύτηκε: Παρ Σεπ 15, 2017 9:52 pm
Δίνονται οι κύκλοι  οι οποίοι εφάπτονται εσωτερικά στο
οι οποίοι εφάπτονται εσωτερικά στο  και η
και η
κοινή τους εφαπτομένη στο σημείο αυτό. Από σημείο της εφαπτομένης αυτής
της εφαπτομένης αυτής
φέρνω εφαπτομένες προς τους και ονομάζω
και ονομάζω  και
και  τα σημεία
τα σημεία
επαφής αντίστοιχα. Η και η
και η  τέμνουν τον
τέμνουν τον 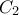 στα
στα  αντιστοίχως.
αντιστοίχως.
Δείξτε ότι τα είναι διαμετρικά σημεία του
είναι διαμετρικά σημεία του 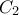 και ότι
και ότι  .
.
 οι οποίοι εφάπτονται εσωτερικά στο
οι οποίοι εφάπτονται εσωτερικά στο  και η
και ηκοινή τους εφαπτομένη στο σημείο αυτό. Από σημείο
 της εφαπτομένης αυτής
της εφαπτομένης αυτήςφέρνω εφαπτομένες προς τους
 και ονομάζω
και ονομάζω  και
και  τα σημεία
τα σημείαεπαφής αντίστοιχα. Η
 και η
και η  τέμνουν τον
τέμνουν τον 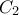 στα
στα  αντιστοίχως.
αντιστοίχως.Δείξτε ότι τα
 είναι διαμετρικά σημεία του
είναι διαμετρικά σημεία του 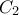 και ότι
και ότι  .
. ή
ή  .
. οι οποίοι εφάπτονται εσωτερικά στο
οι οποίοι εφάπτονται εσωτερικά στο  και
και  τα σημεία επαφής αντίστοιχα. Η
τα σημεία επαφής αντίστοιχα. Η  και η
και η  τέμνουν τον
τέμνουν τον  στα
στα  .
.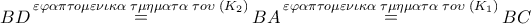 και συνεπώς ο κύκλος με κέντρο
και συνεπώς ο κύκλος με κέντρο 





 . Επίσης αν
. Επίσης αν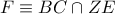 τότε από
τότε από 

 εγγράψιμο σε κύκλο , οπότε
εγγράψιμο σε κύκλο , οπότε 
 και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί.  (εφαπτόμενα τμήματα στους δύο κύκλους) θα είναι
(εφαπτόμενα τμήματα στους δύο κύκλους) θα είναι  όπου
όπου 
 αντίστοιχα (ύψη ισοσκελώς στις «βάσεις» τους άρα και διάμεσοι).
αντίστοιχα (ύψη ισοσκελώς στις «βάσεις» τους άρα και διάμεσοι).  θα είναι
θα είναι  .
.  σύμφωνα με το
σύμφωνα με το  και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί.