 πρώτων όρων δυο αριθμητικών προόδων
πρώτων όρων δυο αριθμητικών προόδων  είναι ίσος με
είναι ίσος με  , για κάθε
, για κάθε  .
.Να βρεθεί ο
 , ώστε ο λόγος
, ώστε ο λόγος  να είναι ακέραιος .
να είναι ακέραιος .Συντονιστής: stranton
 πρώτων όρων δυο αριθμητικών προόδων
πρώτων όρων δυο αριθμητικών προόδων  είναι ίσος με
είναι ίσος με  , για κάθε
, για κάθε  .
. , ώστε ο λόγος
, ώστε ο λόγος  να είναι ακέραιος .
να είναι ακέραιος . οι διαφορές των
οι διαφορές των  αντίστοιχα.
αντίστοιχα.  .
.
 .
.
 , αλλιώς θα είχαμε τριτοβάθμιο πολυώνυμο με άπειρες ρίζες.
, αλλιώς θα είχαμε τριτοβάθμιο πολυώνυμο με άπειρες ρίζες. και άρα αυτό που θέλαμε.
και άρα αυτό που θέλαμε. .
. .
. και άρα ο λόγος δεν μπορεί να έχει ακέραια τιμή.
και άρα ο λόγος δεν μπορεί να έχει ακέραια τιμή. ,οπότε μοναδική δεκτή τιμή η
,οπότε μοναδική δεκτή τιμή η 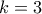 .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 9 επισκέπτες