 πραγματικοί για τους οποίους ισχύουν
πραγματικοί για τους οποίους ισχύουν  και
και 
τότε να δείξετε ότι
1)

2)

Συντονιστής: stranton
 πραγματικοί για τους οποίους ισχύουν
πραγματικοί για τους οποίους ισχύουν  και
και 


Έξυπνη!ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Κυρ Αύγ 09, 2020 11:31 amΑνπραγματικοί για τους οποίους ισχύουν
και
τότε να δείξετε ότι
1)
2)
 . Τότε
. Τότε  και
και  (είναι
(είναι  , οπότε
, οπότε  ). Αν
). Αν  τότε
τότε  , άτοπο. Επίσης αν
, άτοπο. Επίσης αν  τότε
τότε  , άτοπο. Έστω λοιπόν
, άτοπο. Έστω λοιπόν  .
. , άρα αρκεί να δείξω ότι
, άρα αρκεί να δείξω ότι  , δηλαδή ότι
, δηλαδή ότι  . Έστω πως
. Έστω πως  . Τότε,
. Τότε, , άτοπο.
, άτοπο. , άρα αρκεί
, άρα αρκεί  , ή αλλιώς ότι
, ή αλλιώς ότι  . Όμως, είναι
. Όμως, είναι , καθώς
, καθώς  .
.


 κλπ
κλπΑλλιώς: ΕίναιΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Κυρ Αύγ 09, 2020 11:31 amΑνπραγματικοί για τους οποίους ισχύουν
και
τότε να δείξετε ότι
1)
2)
 (αλλιώς η δοθείσα δίνει
(αλλιώς η δοθείσα δίνει  που δεν το επιτρέπει η υπόθεση). Θέτουμε
που δεν το επιτρέπει η υπόθεση). Θέτουμε  , οπότε
, οπότε  . H υπόθεση γίνεται
. H υπόθεση γίνεται  , ισοδύναμα
, ισοδύναμα  και άρα
και άρα  .
.
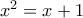 και του
και του  :
:

 στην θέση του δικού μου
στην θέση του δικού μου  ).
).Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες