Να λυθεί η παρακάτω εξίσωση στους πραγματικούς:
 Φιλικά,
Φιλικά,Μάριος
Συντονιστής: stranton
 Φιλικά,
Φιλικά,Αφήνω τις λεπτομέρειες σε κάποιο άλλο μέλος του
 . Άρα η εξίσωση γίνεται:
. Άρα η εξίσωση γίνεται: Ο πίνακας προσήμου είναι ο ακόλουθος:
Ο πίνακας προσήμου είναι ο ακόλουθος:

 . Άλλο ερώτημα : βρείτε τις εφαπτόμενες των γωνιών του
. Άλλο ερώτημα : βρείτε τις εφαπτόμενες των γωνιών του  .
.Αντιθέτως νομίζω ότι είναι πολύ κακό θέμα γιατί κάνεις πολλές φορές τα ίδια ακριβώς ανιαρά βήματα. Πάει περίπατο η φινέτσα των Μαθηματικών.Tolaso J Kos έγραψε: ↑Σάβ Δεκ 22, 2018 12:33 pmΑς βάλει κάποιος μια αναλυτική λύση στο ωραίο αυτό θέμα.
 οπότε η εξίσωση γίνεται
οπότε η εξίσωση γίνεται
 και η
και η  είναι λύση) , αρκεί να λύσουμε την εξίσωση για
είναι λύση) , αρκεί να λύσουμε την εξίσωση για  , και άρα στα
, και άρα στα ![[0,1], [1,\infty] [0,1], [1,\infty]](/forum/ext/geomar/texintegr/latexrender/pictures/a6eec16de4f39af36b7e7a9b69a803af.png) .
. (απορρίπτεται) και στο δεύτερο
(απορρίπτεται) και στο δεύτερο 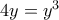 (από τις ρίζες
(από τις ρίζες 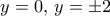 κρατάμε μόνο την
κρατάμε μόνο την  ) .
) .Καλησπέρα σε όλους.
 με
με 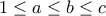 .
. .
. , η εξίσωση είναι αδύνατη, oπότε
, η εξίσωση είναι αδύνατη, oπότε 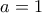 .
.
 ή
ή  η εξίσωση είναι αδύνατη, oπότε
η εξίσωση είναι αδύνατη, oπότε  , από όπου προκύπτει
, από όπου προκύπτει  .
. ,
,  ,
,  .
. .
. .
.Ένα ακόμη εκτός φακέλου ερώτημα : Εξετάστε αν υπάρχει κατακόρυφη ευθεία , η οποία να είναι
 .
. .
.Ο τρόπος που έγραψα την λύση της αρχικής εξίσωσης, παραπάνω, ουσιαστικά απαντάει στα ερωτήματα. Συγκεκριμένα, η αλλαγή μεταβλητής
 (ίσον, μεταφορά αξόνων), τις μετατρέπει στις
(ίσον, μεταφορά αξόνων), τις μετατρέπει στις 
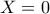 είναι κατακόρυφος άξονας συμμετρίας. Το γράφημα της πρώτης σχεδιάζεται απλά στα διαστήματα
είναι κατακόρυφος άξονας συμμετρίας. Το γράφημα της πρώτης σχεδιάζεται απλά στα διαστήματα ![[0,1], [1, +\infty ) [0,1], [1, +\infty )](/forum/ext/geomar/texintegr/latexrender/pictures/1e5564a9a57598d85ee3cf05a77bee7c.png) (τμήματα ευθειών που συνδέουν τα
(τμήματα ευθειών που συνδέουν τα  ) και συμμετρικά από εκεί και πέρα.
) και συμμετρικά από εκεί και πέρα.Καλησπέρα στην εκλεκτή ομήγυρη του
Και τι να πω για την ... μαφιόζικη "παρέμβαση" εκτός φακέλου αλλά εντός κλίματος από τον κ.KARKAR ! Καταπληκτική!Mihalis_Lambrou έγραψε: ↑Σάβ Δεκ 22, 2018 4:36 pm
Για αναλυτική λύση γλιτώνουμε τα μισά βήματα, και τον πίνακα, αν θέσουμεοπότε η εξίσωση γίνεται
Επειδή τώρα έχουμε συμμετρία (για κάθε λύσηκαι η
είναι λύση) , αρκεί να λύσουμε την εξίσωση για
, και άρα στα
.
Στο πρώτο η εξίσωση γίνεται(απορρίπτεται) και στο δεύτερο
(από τις ρίζες
κρατάμε μόνο την
) .
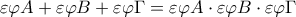 .
.Σταμ. Γλάρος έγραψε: ↑Δευ Δεκ 24, 2018 2:06 pm
Να αποδειχθεί ότι σε κάθε μη ορθογώνιο τρίγωνοισχύει :
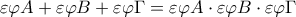



Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες