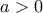 να βρεθή
να βρεθή 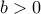 τέτοιο ώστε ;
τέτοιο ώστε ;Εαν
 , τότε
, τότε 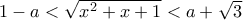
Συντονιστής: stranton
Για λόγους ευκολίας την
 την γράφω
την γράφω 
 γίνεται
γίνεται 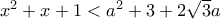
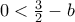 αρκεί να είναι
αρκεί να είναι 
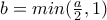 ισχύει.
ισχύει.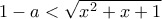 για
για 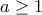 ισχύει για οποιαδήποτε επιλογή του
ισχύει για οποιαδήποτε επιλογή του  .
.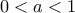 γίνεται
γίνεται 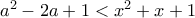
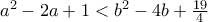
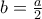 .(αφού
.(αφού 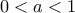
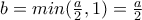
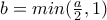
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 11 επισκέπτες