Να δείξετε ότι

Συντονιστές: Demetres, socrates, silouan

 (αλλιώς για
(αλλιώς για  το
το 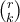 δεν έχει νόημα) και
δεν έχει νόημα) και  (αλλιώς για
(αλλιώς για  το
το  δεν έχει νόημα).
δεν έχει νόημα).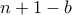 στοιχεία από το σύνολο
στοιχεία από το σύνολο  ώστε το
ώστε το  -οστό στοιχείο να είναι το
-οστό στοιχείο να είναι το  .
.  στοιχεία πρέπει να επιλέξουμε τα
στοιχεία πρέπει να επιλέξουμε τα  και από τα τελευταία
και από τα τελευταία  πρέπει να επιλέξουμε τα
πρέπει να επιλέξουμε τα  . Επομένως υπάρχουν
. Επομένως υπάρχουν 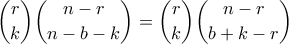
 και
και 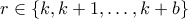 . Το μόνο που δεν είναι προφανές είναι ότι
. Το μόνο που δεν είναι προφανές είναι ότι 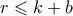 . Για να το δούμε παρατηρούμε ότι πρέπει στα τελευταία
. Για να το δούμε παρατηρούμε ότι πρέπει στα τελευταία  στοιχεία να επιλέξουμε
στοιχεία να επιλέξουμε  επομένως θέλουμε
επομένως θέλουμε  .
.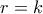 ως
ως  για να πάρουμε
για να πάρουμε
Έχοντας δει παρόμοια σε γενήτριες συναρτήσεις (άσκηση στο κεφάλαιο δηλαδή), μπορεί αυτό να δειχθεί με τη χρήση γενήτριας συνάρτησης;Λάμπρος Κατσάπας έγραψε: ↑Δευ Απρ 13, 2020 1:17 amΜου προέκυψε από κατασκευή μοντέλου δειγματοληψίας. Ενδεχομένως να έχει ξανατεθεί εδώ στο.
Να δείξετε ότι
Γεια!miltosk έγραψε: ↑Δευ Απρ 13, 2020 4:15 pmΈχοντας δει παρόμοια σε γενήτριες συναρτήσεις (άσκηση στο κεφάλαιο δηλαδή), μπορεί αυτό να δειχθεί με τη χρήση γενήτριας συνάρτησης;Λάμπρος Κατσάπας έγραψε: ↑Δευ Απρ 13, 2020 1:17 amΜου προέκυψε από κατασκευή μοντέλου δειγματοληψίας. Ενδεχομένως να έχει ξανατεθεί εδώ στο.
Να δείξετε ότι
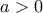 είναι
είναι 


Ας μείνω στη συνδυαστική προσέγγιση γ λυκείου είμαι αλλά ευχαριστώ για το ενδιαφέρον.Λάμπρος Κατσάπας έγραψε: ↑Δευ Απρ 13, 2020 6:44 pmΓεια!miltosk έγραψε: ↑Δευ Απρ 13, 2020 4:15 pmΈχοντας δει παρόμοια σε γενήτριες συναρτήσεις (άσκηση στο κεφάλαιο δηλαδή), μπορεί αυτό να δειχθεί με τη χρήση γενήτριας συνάρτησης;Λάμπρος Κατσάπας έγραψε: ↑Δευ Απρ 13, 2020 1:17 amΜου προέκυψε από κατασκευή μοντέλου δειγματοληψίας. Ενδεχομένως να έχει ξανατεθεί εδώ στο.
Να δείξετε ότι
Υπόδειξη:
1) Γιαείναι
2) Διακριτή συνέλιξη - Cauchy product.
3)
4) Άλλαξε τη σειρά άθροισης να ξεκινά από το
* Είναι ''γεννήτρια''.
Νόμιζα ότι μιλούσα με φοιτητή. Θα σου γράψω μια λύση βασισμένη στην υπόδειξη το συντομότερο δυνατό. Δεν έχω internet και αναγκάζομαι να γράφω από κινητό.Ας μείνω στη συνδυαστική προσέγγιση γ λυκείου είμαι αλλά ευχαριστώ για το ενδιαφέρον.
 βρίσκουμε ότι το άθροισμά μας γράφεται
βρίσκουμε ότι το άθροισμά μας γράφεται


![\displaystyle=\left [\sum_{j=0}^{\infty }(-1)^j\binom{-(k+1)}{j}x^j \right ] \cdot \left [\sum_{l=0}^{\infty }(-1)^l\binom{-(n-b-k+1)}{l}x^l \right ] \displaystyle=\left [\sum_{j=0}^{\infty }(-1)^j\binom{-(k+1)}{j}x^j \right ] \cdot \left [\sum_{l=0}^{\infty }(-1)^l\binom{-(n-b-k+1)}{l}x^l \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/7597cb71f8f8ab297d4590d1864113af.png)


 γίνεται
γίνεται 

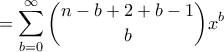

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης