 κούτες, στις οποίες συνολικά υπάρχουν από όλα τα πορτοκάλια τουλάχιστον τα μισά, από όλα τα μήλα τουλάχιστον τα μισά και από όλες τις μπανάνες τουλάχιστον οι μισές.
κούτες, στις οποίες συνολικά υπάρχουν από όλα τα πορτοκάλια τουλάχιστον τα μισά, από όλα τα μήλα τουλάχιστον τα μισά και από όλες τις μπανάνες τουλάχιστον οι μισές.Φρουτεμπορική
Συντονιστές: Demetres, socrates, silouan
- Al.Koutsouridis
- Δημοσιεύσεις: 1797
- Εγγραφή: Πέμ Ιαν 30, 2014 11:58 pm
- Τοποθεσία: Αθήνα
Φρουτεμπορική
Σε εκατό κούτες είναι τοποθετημένα πορτοκάλια, μήλα και μπανάνες. Αποδείξτε ότι μπορούμε να διαλέξουμε  κούτες, στις οποίες συνολικά υπάρχουν από όλα τα πορτοκάλια τουλάχιστον τα μισά, από όλα τα μήλα τουλάχιστον τα μισά και από όλες τις μπανάνες τουλάχιστον οι μισές.
κούτες, στις οποίες συνολικά υπάρχουν από όλα τα πορτοκάλια τουλάχιστον τα μισά, από όλα τα μήλα τουλάχιστον τα μισά και από όλες τις μπανάνες τουλάχιστον οι μισές.
 κούτες, στις οποίες συνολικά υπάρχουν από όλα τα πορτοκάλια τουλάχιστον τα μισά, από όλα τα μήλα τουλάχιστον τα μισά και από όλες τις μπανάνες τουλάχιστον οι μισές.
κούτες, στις οποίες συνολικά υπάρχουν από όλα τα πορτοκάλια τουλάχιστον τα μισά, από όλα τα μήλα τουλάχιστον τα μισά και από όλες τις μπανάνες τουλάχιστον οι μισές.Λέξεις Κλειδιά:
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: Φρουτεμπορική
Δίνω μια απόδειξη η οποία χρησιμοποιεί ένα μη στοιχειώδες θεώρημα. Θα ενδιαφερόμουν αν δω αν υπάρχει κάτι άλλο.
Αριθμούμε τις κούτες από το ως το
ως το  . Αν δεν ισχύει το ζητούμενο, για κάθε υποσύνολο
. Αν δεν ισχύει το ζητούμενο, για κάθε υποσύνολο  του
του  υπάρχει ένα φρούτο ώστε οι αντίστοιχες κούτες να περιέχουν λιγότερα από τα μισά φρούτα αυτού του είδους. Τότε οι αντίστοιχες κούτες του
υπάρχει ένα φρούτο ώστε οι αντίστοιχες κούτες να περιέχουν λιγότερα από τα μισά φρούτα αυτού του είδους. Τότε οι αντίστοιχες κούτες του  περιέχουν περισσότερα από τα μισά φρούτα αυτού του είδους.
περιέχουν περισσότερα από τα μισά φρούτα αυτού του είδους.
Κατασκευάζουμε τώρα ένα γράφημα με κορυφές τα υποσύνολα του μεγέθους
μεγέθους  όπου συνδέουμε
όπου συνδέουμε  με ακμή αν και μόνο αν είναι ξένα μεταξύ τους. Από γνωστό θεώρημα (*) ο χρωματικός αριθμός αυτού του γραφήματος είναι
με ακμή αν και μόνο αν είναι ξένα μεταξύ τους. Από γνωστό θεώρημα (*) ο χρωματικός αριθμός αυτού του γραφήματος είναι  .
.
Αυτό σημαίνει ότι θα υπάρχουν δύο ξένα μεταξύ τους σύνολα μεγέθους
μεγέθους  και ένα συγκεκριμένο φρούτο, έστω πορτοκάλι, ώστε στα αντίστοιχα κουτιά των
και ένα συγκεκριμένο φρούτο, έστω πορτοκάλι, ώστε στα αντίστοιχα κουτιά των  και
και  τα πορτοκάλια να είναι περισσότερα από τα μισά. Αυτό όμως είναι άτοπο αφού τότε στην ένωση των
τα πορτοκάλια να είναι περισσότερα από τα μισά. Αυτό όμως είναι άτοπο αφού τότε στην ένωση των  θα είχαμε περισσότερα πορτοκάλια από όσα υπάρχουν.
θα είχαμε περισσότερα πορτοκάλια από όσα υπάρχουν.
(*) Η εικασία του Kneser λέει ότι το γράφημα με κορυφές τα υποσύνολα του μεγέθους
μεγέθους  όπου συνδέουμε δύο μεταξύ τους αν και μόνο αν είναι ξένα μεταξύ τους έχει χρωματικό αριθμό
όπου συνδέουμε δύο μεταξύ τους αν και μόνο αν είναι ξένα μεταξύ τους έχει χρωματικό αριθμό  . Ένας χρωματισμός με τόσα χρώματα είναι ο εξής: Χρωματίζουμε όλα τα
. Ένας χρωματισμός με τόσα χρώματα είναι ο εξής: Χρωματίζουμε όλα τα  -σύνολα που περιέχουν το
-σύνολα που περιέχουν το  με το χρώμα
με το χρώμα  . Χρωματίζουμε όλα τα
. Χρωματίζουμε όλα τα  -σύνολα που περιέχουν το
-σύνολα που περιέχουν το  αλλά όχι το
αλλά όχι το  με το χρώμα
με το χρώμα  κ.ο.κ. μέχρι να χρωματίσουμε όλα τα
κ.ο.κ. μέχρι να χρωματίσουμε όλα τα  -σύνολα που περιέχουν το
-σύνολα που περιέχουν το  αλλά όχι τα
αλλά όχι τα  με το χρώμα
με το χρώμα  . Τέλος χρωματίζουμε όλα τα υπόλοιπα σύνολα (ανά δύο δεν είναι ξένα μεταξύ τους) με το χρώμα
. Τέλος χρωματίζουμε όλα τα υπόλοιπα σύνολα (ανά δύο δεν είναι ξένα μεταξύ τους) με το χρώμα  . Η εικασία αποδείχθηκε από τον Lovász χρησιμοποιώντας ένα τοπολογικό θεώρημα (το θεώρημα Borsuk-Ulam). Για τη συγκεκριμένη περίπτωση που χρησιμοποίησα θέλουμε την περίπτωση του θεωρήματος στην 3-διάστατη σφαίρα το οποίο δεν είναι στοιχειώδες να αποδειχθεί.
. Η εικασία αποδείχθηκε από τον Lovász χρησιμοποιώντας ένα τοπολογικό θεώρημα (το θεώρημα Borsuk-Ulam). Για τη συγκεκριμένη περίπτωση που χρησιμοποίησα θέλουμε την περίπτωση του θεωρήματος στην 3-διάστατη σφαίρα το οποίο δεν είναι στοιχειώδες να αποδειχθεί.
Αριθμούμε τις κούτες από το
 ως το
ως το  . Αν δεν ισχύει το ζητούμενο, για κάθε υποσύνολο
. Αν δεν ισχύει το ζητούμενο, για κάθε υποσύνολο  του
του  υπάρχει ένα φρούτο ώστε οι αντίστοιχες κούτες να περιέχουν λιγότερα από τα μισά φρούτα αυτού του είδους. Τότε οι αντίστοιχες κούτες του
υπάρχει ένα φρούτο ώστε οι αντίστοιχες κούτες να περιέχουν λιγότερα από τα μισά φρούτα αυτού του είδους. Τότε οι αντίστοιχες κούτες του  περιέχουν περισσότερα από τα μισά φρούτα αυτού του είδους.
περιέχουν περισσότερα από τα μισά φρούτα αυτού του είδους.Κατασκευάζουμε τώρα ένα γράφημα με κορυφές τα υποσύνολα του
 μεγέθους
μεγέθους  όπου συνδέουμε
όπου συνδέουμε  με ακμή αν και μόνο αν είναι ξένα μεταξύ τους. Από γνωστό θεώρημα (*) ο χρωματικός αριθμός αυτού του γραφήματος είναι
με ακμή αν και μόνο αν είναι ξένα μεταξύ τους. Από γνωστό θεώρημα (*) ο χρωματικός αριθμός αυτού του γραφήματος είναι  .
.Αυτό σημαίνει ότι θα υπάρχουν δύο ξένα μεταξύ τους σύνολα
 μεγέθους
μεγέθους  και ένα συγκεκριμένο φρούτο, έστω πορτοκάλι, ώστε στα αντίστοιχα κουτιά των
και ένα συγκεκριμένο φρούτο, έστω πορτοκάλι, ώστε στα αντίστοιχα κουτιά των  και
και  τα πορτοκάλια να είναι περισσότερα από τα μισά. Αυτό όμως είναι άτοπο αφού τότε στην ένωση των
τα πορτοκάλια να είναι περισσότερα από τα μισά. Αυτό όμως είναι άτοπο αφού τότε στην ένωση των  θα είχαμε περισσότερα πορτοκάλια από όσα υπάρχουν.
θα είχαμε περισσότερα πορτοκάλια από όσα υπάρχουν.(*) Η εικασία του Kneser λέει ότι το γράφημα με κορυφές τα υποσύνολα του
 μεγέθους
μεγέθους  όπου συνδέουμε δύο μεταξύ τους αν και μόνο αν είναι ξένα μεταξύ τους έχει χρωματικό αριθμό
όπου συνδέουμε δύο μεταξύ τους αν και μόνο αν είναι ξένα μεταξύ τους έχει χρωματικό αριθμό  . Ένας χρωματισμός με τόσα χρώματα είναι ο εξής: Χρωματίζουμε όλα τα
. Ένας χρωματισμός με τόσα χρώματα είναι ο εξής: Χρωματίζουμε όλα τα  -σύνολα που περιέχουν το
-σύνολα που περιέχουν το  με το χρώμα
με το χρώμα  . Χρωματίζουμε όλα τα
. Χρωματίζουμε όλα τα  -σύνολα που περιέχουν το
-σύνολα που περιέχουν το  αλλά όχι το
αλλά όχι το  με το χρώμα
με το χρώμα  κ.ο.κ. μέχρι να χρωματίσουμε όλα τα
κ.ο.κ. μέχρι να χρωματίσουμε όλα τα  -σύνολα που περιέχουν το
-σύνολα που περιέχουν το  αλλά όχι τα
αλλά όχι τα  με το χρώμα
με το χρώμα  . Τέλος χρωματίζουμε όλα τα υπόλοιπα σύνολα (ανά δύο δεν είναι ξένα μεταξύ τους) με το χρώμα
. Τέλος χρωματίζουμε όλα τα υπόλοιπα σύνολα (ανά δύο δεν είναι ξένα μεταξύ τους) με το χρώμα  . Η εικασία αποδείχθηκε από τον Lovász χρησιμοποιώντας ένα τοπολογικό θεώρημα (το θεώρημα Borsuk-Ulam). Για τη συγκεκριμένη περίπτωση που χρησιμοποίησα θέλουμε την περίπτωση του θεωρήματος στην 3-διάστατη σφαίρα το οποίο δεν είναι στοιχειώδες να αποδειχθεί.
. Η εικασία αποδείχθηκε από τον Lovász χρησιμοποιώντας ένα τοπολογικό θεώρημα (το θεώρημα Borsuk-Ulam). Για τη συγκεκριμένη περίπτωση που χρησιμοποίησα θέλουμε την περίπτωση του θεωρήματος στην 3-διάστατη σφαίρα το οποίο δεν είναι στοιχειώδες να αποδειχθεί.- Al.Koutsouridis
- Δημοσιεύσεις: 1797
- Εγγραφή: Πέμ Ιαν 30, 2014 11:58 pm
- Τοποθεσία: Αθήνα
Re: Φρουτεμπορική
Το πρόβλημα είναι το υπ’ αριθμόν 4830 του περιοδικού «Τα μαθηματικά στο σχολείο», τεύχος 4, 2005. Η λύση που δίνεται στο περιοδικό είναι η παρακάτω.
Λήμμα: Απόδειξη: Λύση:
Σκιαγραφείτε και μια δεύτερη λύση ( από αναγνώστη) ως σχόλιο με παρόμοια (ίδια) ιδέα με αυτή που περιέγραψε ο κ. Δημήτρης παραπάνω.
Η λύση αυτή στηρίζεται στο λεγόμενο Ham sandwich theorem: για οποιαδήποτε τρία σώματα στο χώρο υπάρχει επίπεδο, που διαιρεί τον όγκο καθενός εξ αυτών των σωμάτων στο ήμισυ. Τοποθετούμε τις κούτες στο χώρο έτσι, ώστε κανένα επίπεδο να μην τέμνει πάνω από τρεις κούτες. Ως σώματα θα θεωρήσουμε την ένωση όλων των πορτοκαλιών, την ένωση όλων των μήλων και την ένωση όλων των μπανανών. Τώρα αν φέρουμε το επίπεδο που διαιρεί και τα τρία σώματα κατά το ήμισυ, τότε στη μια πλευρά αυτού θα βρεθούν τουλάχιστον
 κούτες. Διαλέγοντας, όλες τις κούτες εκτός από αυτές, προκύπτει η ζητούμενη ομάδα κουτών. Σημειώνεται επίσης ότι στη γενίκευση του προβλήματος για
κούτες. Διαλέγοντας, όλες τις κούτες εκτός από αυτές, προκύπτει η ζητούμενη ομάδα κουτών. Σημειώνεται επίσης ότι στη γενίκευση του προβλήματος για 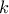 είδη φρούτων και για αρκούντος μεγάλο αριθμό κουτών
είδη φρούτων και για αρκούντος μεγάλο αριθμό κουτών  η απάντηση είναι ο ελάχιστος ακέραιος που δεν είναι μικρότερος του
η απάντηση είναι ο ελάχιστος ακέραιος που δεν είναι μικρότερος του  .
.Το πρόβλημα μου άρεσε αρκετά, άλλωστε ψηφίστηκε από τους αναγνώστες ως το καλύτερο της χρονιάς, και είπα να το μοιραστώ.
Για τους ανήσυχους υπάρχει το βιβλίο Using the Borsuk-Ulam theorem, Matousek J., που φαίνεται να είναι ενδιαφέρον και διαπραγματεύεται τοπολογικές μεθόδους στην επίλυση προβλημάτων συνδιαστικής.
Υπάρχει και το φυλλάδιο "Εικασία του Kneser και τοπολογικές μέθοδοι στην συνδιαστική" δυστυχώς στα ρωσικά, που διαπαραγματεύεται μερικές από τις ιδέες που ανέφερε ο κ.Δημήτρης στην λύση του με ποιο εκλαϊκευμένο τρόπο. (το φυλλάδιο είναι για μαθητές καλοκαιρινού σχολείου)
τελευταία επεξεργασία από Al.Koutsouridis σε Τετ Αύγ 14, 2019 7:45 pm, έχει επεξεργασθεί 3 φορές συνολικά.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες

 κούτες, το πλήθος των πορτοκαλιών και μήλων σε κάθε μία από τις οποίες δεν υπερβαίνει το
κούτες, το πλήθος των πορτοκαλιών και μήλων σε κάθε μία από τις οποίες δεν υπερβαίνει το  κουτών έτσι, ώστε αυτές οι ομάδες να διαφέρουν το πολύ κατά
κουτών έτσι, ώστε αυτές οι ομάδες να διαφέρουν το πολύ κατά 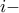 οστή (
οστή ( ) κούτα θα το συμβολίσουμε με
) κούτα θα το συμβολίσουμε με  και
και  αντίστοιχα. Εξάλλου θα θεωρήσουμε ότι
αντίστοιχα. Εξάλλου θα θεωρήσουμε ότι 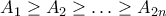 .
.  (
( ), προσθέτουμε στις διάφορες ομάδες κουτών τις κούτες με νούμερα
), προσθέτουμε στις διάφορες ομάδες κουτών τις κούτες με νούμερα  και
και  , μάλιστα εκείνη από αυτές, στην οποία τα μήλα δεν είναι λιγότερα από την άλλη, προστίθεται σε εκείνη την ομάδα, όπου τα μήλα δεν είναι περισσότερα, από την άλλη.
, μάλιστα εκείνη από αυτές, στην οποία τα μήλα δεν είναι λιγότερα από την άλλη, προστίθεται σε εκείνη την ομάδα, όπου τα μήλα δεν είναι περισσότερα, από την άλλη. .
. (
( ) η διαφορά την χρονική στιγμή κατά την οποία στις ομάδες προστίθενται οι κούτες με νούμερα από
) η διαφορά την χρονική στιγμή κατά την οποία στις ομάδες προστίθενται οι κούτες με νούμερα από  και αν
και αν  , τότε
, τότε  . Από την αρχή της μαθηματικής επαγωγής
. Από την αρχή της μαθηματικής επαγωγής  . Το λήμμα αποδείχθηκε.
. Το λήμμα αποδείχθηκε.  απομείναντες εκείνη, στην οποία τα μήλα δεν είναι λιγότερα από κάθε μια από τις
απομείναντες εκείνη, στην οποία τα μήλα δεν είναι λιγότερα από κάθε μια από τις  απομείναντες. Στη συνέχεια με την διαδικασία που υποδείχτηκε στην απόδειξη του λήμματος διαιρούμε τις
απομείναντες. Στη συνέχεια με την διαδικασία που υποδείχτηκε στην απόδειξη του λήμματος διαιρούμε τις  κούτες, έχουμε διαλέξει τουλάχιστον το μισό αριθμό των συνολικών πορτοκαλιών, τουλάχιστον το μισό συνολικό αριθμό των μήλων και τουλάχιστον το μισό συνολικό αριθμό μπανανών.
κούτες, έχουμε διαλέξει τουλάχιστον το μισό αριθμό των συνολικών πορτοκαλιών, τουλάχιστον το μισό συνολικό αριθμό των μήλων και τουλάχιστον το μισό συνολικό αριθμό μπανανών.