Περίπτωση 1:
Αν

και

τότε χρωματίζουμε τα τετράγωνα της πλατείας όπως την σκακιέρα. Κάθε τετράγωνο θέλει τουλάχιστον δύο φανάρια. Επίσης δεν μπορεί ένα φανάρι να φωτίζει τετράγωνα διαφορετικού χρώματος. Επειδή έχουμε

τετράγωνα του ιδίου χρώματος χρειαζόμαστε τουλάχιστον

φανάρια. Η κατασκευή του Διονύση δείχνει ότι μπορούμε να έχουμε τόσα φανάρια.
Περίπτωση 2:
Αν

και

τότε πάλι χρωματίζουμε όπως στην σκακιέρα. Τώρα έχουμε

τετράγωνα του ιδίου χρώματος που θέλουν

φανάρια. Πάλι αυτό επιτυγχάνεται από την κατασκευή του Διονύση.
Περίπτωση 3: Αν

άρτιος,

περιττός αντιμετωπίζεται όπως στην περίπτωση 2.
Περίπτωση 4: Αν

τότε χρωματίζουμε την πλατεία όπως στην πιο κάτω εικόνα (για

.)
![\begin{tikzpicture}[line cap=round,line join=round,>=triangle 45,x=1.0cm,y=1.0cm]
\clip(-0.52,-0.46) rectangle (6.44,4.44);
\fill[fill=black,fill opacity=1.0] (0.,4.) -- (0.,3.) -- (1.,3.) -- (1.,4.) -- cycle;
\fill[fill=black,fill opacity=1.0] (2.,4.) -- (2.,3.) -- (3.,3.) -- (3.,4.) -- cycle;
\fill[fill=black,fill opacity=1.0] (4.,4.) -- (4.,3.) -- (5.,3.) -- (5.,4.) -- cycle;
\fill[fill=black,fill opacity=1.0] (5.,3.) -- (5.,2.) -- (6.,2.) -- (6.,3.) -- cycle;
\fill[fill=black,fill opacity=1.0] (0.,2.) -- (0.,1.) -- (1.,1.) -- (1.,2.) -- cycle;
\fill[fill=black,fill opacity=1.0] (2.,2.) -- (2.,1.) -- (3.,1.) -- (3.,2.) -- cycle;
\fill[fill=black,fill opacity=1.0] (3.,1.) -- (3.,0.) -- (4.,0.) -- (4.,1.) -- cycle;
\fill[fill=black,fill opacity=1.0] (5.,1.) -- (5.,0.) -- (6.,0.) -- (6.,1.) -- cycle;
\draw (0.,0.)-- (0.,4.);
\draw (0.,4.)-- (6.,4.);
\draw (6.,4.)-- (6.,0.);
\draw (6.,0.)-- (0.,0.);
\draw (0.,3.)-- (6.,3.);
\draw (0.,2.)-- (6.,2.);
\draw (0.,1.)-- (6.,1.);
\draw (1.,4.)-- (1.,0.);
\draw (2.,0.)-- (2.,4.);
\draw (3.,4.)-- (3.,0.);
\draw (4.,0.)-- (4.,4.);
\draw (5.,4.)-- (5.,0.);
\draw (0.,4.)-- (0.,3.);
\draw (0.,3.)-- (1.,3.);
\draw (1.,3.)-- (1.,4.);
\draw (1.,4.)-- (0.,4.);
\draw (2.,4.)-- (2.,3.);
\draw (2.,3.)-- (3.,3.);
\draw (3.,3.)-- (3.,4.);
\draw (3.,4.)-- (2.,4.);
\draw (4.,4.)-- (4.,3.);
\draw (4.,3.)-- (5.,3.);
\draw (5.,3.)-- (5.,4.);
\draw (5.,4.)-- (4.,4.);
\draw (5.,3.)-- (5.,2.);
\draw (5.,2.)-- (6.,2.);
\draw (6.,2.)-- (6.,3.);
\draw (6.,3.)-- (5.,3.);
\draw (0.,2.)-- (0.,1.);
\draw (0.,1.)-- (1.,1.);
\draw (1.,1.)-- (1.,2.);
\draw (1.,2.)-- (0.,2.);
\draw (2.,2.)-- (2.,1.);
\draw (2.,1.)-- (3.,1.);
\draw (3.,1.)-- (3.,2.);
\draw (3.,2.)-- (2.,2.);
\draw (3.,1.)-- (3.,0.);
\draw (3.,0.)-- (4.,0.);
\draw (4.,0.)-- (4.,1.);
\draw (4.,1.)-- (3.,1.);
\draw (5.,1.)-- (5.,0.);
\draw (5.,0.)-- (6.,0.);
\draw (6.,0.)-- (6.,1.);
\draw (6.,1.)-- (5.,1.);
\end{tikzpicture} \begin{tikzpicture}[line cap=round,line join=round,>=triangle 45,x=1.0cm,y=1.0cm]
\clip(-0.52,-0.46) rectangle (6.44,4.44);
\fill[fill=black,fill opacity=1.0] (0.,4.) -- (0.,3.) -- (1.,3.) -- (1.,4.) -- cycle;
\fill[fill=black,fill opacity=1.0] (2.,4.) -- (2.,3.) -- (3.,3.) -- (3.,4.) -- cycle;
\fill[fill=black,fill opacity=1.0] (4.,4.) -- (4.,3.) -- (5.,3.) -- (5.,4.) -- cycle;
\fill[fill=black,fill opacity=1.0] (5.,3.) -- (5.,2.) -- (6.,2.) -- (6.,3.) -- cycle;
\fill[fill=black,fill opacity=1.0] (0.,2.) -- (0.,1.) -- (1.,1.) -- (1.,2.) -- cycle;
\fill[fill=black,fill opacity=1.0] (2.,2.) -- (2.,1.) -- (3.,1.) -- (3.,2.) -- cycle;
\fill[fill=black,fill opacity=1.0] (3.,1.) -- (3.,0.) -- (4.,0.) -- (4.,1.) -- cycle;
\fill[fill=black,fill opacity=1.0] (5.,1.) -- (5.,0.) -- (6.,0.) -- (6.,1.) -- cycle;
\draw (0.,0.)-- (0.,4.);
\draw (0.,4.)-- (6.,4.);
\draw (6.,4.)-- (6.,0.);
\draw (6.,0.)-- (0.,0.);
\draw (0.,3.)-- (6.,3.);
\draw (0.,2.)-- (6.,2.);
\draw (0.,1.)-- (6.,1.);
\draw (1.,4.)-- (1.,0.);
\draw (2.,0.)-- (2.,4.);
\draw (3.,4.)-- (3.,0.);
\draw (4.,0.)-- (4.,4.);
\draw (5.,4.)-- (5.,0.);
\draw (0.,4.)-- (0.,3.);
\draw (0.,3.)-- (1.,3.);
\draw (1.,3.)-- (1.,4.);
\draw (1.,4.)-- (0.,4.);
\draw (2.,4.)-- (2.,3.);
\draw (2.,3.)-- (3.,3.);
\draw (3.,3.)-- (3.,4.);
\draw (3.,4.)-- (2.,4.);
\draw (4.,4.)-- (4.,3.);
\draw (4.,3.)-- (5.,3.);
\draw (5.,3.)-- (5.,4.);
\draw (5.,4.)-- (4.,4.);
\draw (5.,3.)-- (5.,2.);
\draw (5.,2.)-- (6.,2.);
\draw (6.,2.)-- (6.,3.);
\draw (6.,3.)-- (5.,3.);
\draw (0.,2.)-- (0.,1.);
\draw (0.,1.)-- (1.,1.);
\draw (1.,1.)-- (1.,2.);
\draw (1.,2.)-- (0.,2.);
\draw (2.,2.)-- (2.,1.);
\draw (2.,1.)-- (3.,1.);
\draw (3.,1.)-- (3.,2.);
\draw (3.,2.)-- (2.,2.);
\draw (3.,1.)-- (3.,0.);
\draw (3.,0.)-- (4.,0.);
\draw (4.,0.)-- (4.,1.);
\draw (4.,1.)-- (3.,1.);
\draw (5.,1.)-- (5.,0.);
\draw (5.,0.)-- (6.,0.);
\draw (6.,0.)-- (6.,1.);
\draw (6.,1.)-- (5.,1.);
\end{tikzpicture}](/forum/ext/geomar/texintegr/latexrender/pictures/102dda3d072c1deca91ec59d57018584.png)
Πιο συγκεκριμένα για την πλατεία

με

.
Στην πρώτη σειρά χρωματίζουμε
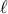
τετράγωνα μαύρα εναλλάξ ξεκινώντας από αριστερά.
Στην τρίτη σειρά χρωματίζουμε

τετράγωνα μαύρα εναλλάξ ξεκινώντας από αριστερά.
...
Στην

σειρά χρωματίζουμε

τετράγωνα μαύρα εναλλάξ ξεκινώντας από αριστερά.
Στην δεύτερη σειρά χρωματίζουμε

τετράγωνο μαύρο ξεκινώντας από δεξιά.
Στην τέταρτη σειρά χρωματίζουμε

τετράγωνα μαύρα ξεκινώντας από δεξιά.
...
Στην

σειρά χρωματίζουμε

τετράγωνα μαύρα ξεκινώντας από δεξιά.
Συνολικά χρωματίσαμε

μαύρα τετράγωνα. Κάθε ένα θέλει από

φανάρια. Μόνο που υπάρχουν

ζεύγη μαύρων τετραγώνων που μαζί αντί

φανάρια θέλουν μόνο

. Συνολικά λοιπόν χρειάζονται

φανάρια. Πάλι η τοποθέτηση του Διονύση χρησιμοποιεί μόνο τόσο φανάρια.
Επεξεργασία: Προσθέτω και την
πηγή.
 αποτελούμενη από
αποτελούμενη από 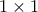 τετράγωνα. Για να φωταγωγηθεί η πλατεία θα τοποθετηθούν φανάρια στις γωνίες των τετραγώνων. (Επιτρέπεται η τοποθέτηση και σε γωνίες των τετραγώνων που βρίσκονται περιμετρικά της πλατείας.) Κάθε φανάρι φωτίζει όλα τα τετράγωνα στα οποία βρίσκεται στην γωνία τους. Θέλουμε να τοποθετήσουμε τα φανάρια με τέτοιο τρόπο ώστε να φωτίζονται όλα τα τετράγωνα ακόμη και αν καεί ένα από τα φανάρια.
τετράγωνα. Για να φωταγωγηθεί η πλατεία θα τοποθετηθούν φανάρια στις γωνίες των τετραγώνων. (Επιτρέπεται η τοποθέτηση και σε γωνίες των τετραγώνων που βρίσκονται περιμετρικά της πλατείας.) Κάθε φανάρι φωτίζει όλα τα τετράγωνα στα οποία βρίσκεται στην γωνία τους. Θέλουμε να τοποθετήσουμε τα φανάρια με τέτοιο τρόπο ώστε να φωτίζονται όλα τα τετράγωνα ακόμη και αν καεί ένα από τα φανάρια. 
 .
.

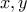 η μεγαλύτερη και η μικρότερη διάσταση αντίστοιχα (ή κάτι τέτοιο... νομίζω με κάποιες περιπτώσεις...).
η μεγαλύτερη και η μικρότερη διάσταση αντίστοιχα (ή κάτι τέτοιο... νομίζω με κάποιες περιπτώσεις...). νομίζω πως αρκούν
νομίζω πως αρκούν  φανάρια αντί για
φανάρια αντί για  που προκύπτουν από την παραπάνω λύση. Θα επανέρθω... όταν βρω λίγο χρόνο...
που προκύπτουν από την παραπάνω λύση. Θα επανέρθω... όταν βρω λίγο χρόνο... χρειάζονται μόνο
χρειάζονται μόνο  φώτα και όχι
φώτα και όχι  . Χώρισέ το όπως είπες σε περιπτώσεις. Δεν είναι ανάγκη να δώσεις έναν τύπο για όλες τις περιπτώσεις.
. Χώρισέ το όπως είπες σε περιπτώσεις. Δεν είναι ανάγκη να δώσεις έναν τύπο για όλες τις περιπτώσεις. (της μικρότερης πλευράς). Αν το
(της μικρότερης πλευράς). Αν το  .
. φανάρια, άρα δεν έχουμε πρόβλημα. Το θέμα είναι ότι κάποιος θα μπορούσε να το κάνει αυτό στις γραμμές και όχι στις στήλες. Το πότε αυτό βολεύει έχει να κάνει με την αρτιότητα του
φανάρια, άρα δεν έχουμε πρόβλημα. Το θέμα είναι ότι κάποιος θα μπορούσε να το κάνει αυτό στις γραμμές και όχι στις στήλες. Το πότε αυτό βολεύει έχει να κάνει με την αρτιότητα του  περιπτώσεις της αρτιότητας ή "περιττότητας" των
περιπτώσεις της αρτιότητας ή "περιττότητας" των  και
και  τότε χρωματίζουμε τα τετράγωνα της πλατείας όπως την σκακιέρα. Κάθε τετράγωνο θέλει τουλάχιστον δύο φανάρια. Επίσης δεν μπορεί ένα φανάρι να φωτίζει τετράγωνα διαφορετικού χρώματος. Επειδή έχουμε
τότε χρωματίζουμε τα τετράγωνα της πλατείας όπως την σκακιέρα. Κάθε τετράγωνο θέλει τουλάχιστον δύο φανάρια. Επίσης δεν μπορεί ένα φανάρι να φωτίζει τετράγωνα διαφορετικού χρώματος. Επειδή έχουμε  τετράγωνα του ιδίου χρώματος χρειαζόμαστε τουλάχιστον
τετράγωνα του ιδίου χρώματος χρειαζόμαστε τουλάχιστον  φανάρια. Η κατασκευή του Διονύση δείχνει ότι μπορούμε να έχουμε τόσα φανάρια.
φανάρια. Η κατασκευή του Διονύση δείχνει ότι μπορούμε να έχουμε τόσα φανάρια. τότε πάλι χρωματίζουμε όπως στην σκακιέρα. Τώρα έχουμε
τότε πάλι χρωματίζουμε όπως στην σκακιέρα. Τώρα έχουμε  τετράγωνα του ιδίου χρώματος που θέλουν
τετράγωνα του ιδίου χρώματος που θέλουν  φανάρια. Πάλι αυτό επιτυγχάνεται από την κατασκευή του Διονύση.
φανάρια. Πάλι αυτό επιτυγχάνεται από την κατασκευή του Διονύση. άρτιος,
άρτιος,  περιττός αντιμετωπίζεται όπως στην περίπτωση 2.
περιττός αντιμετωπίζεται όπως στην περίπτωση 2. τότε χρωματίζουμε την πλατεία όπως στην πιο κάτω εικόνα (για
τότε χρωματίζουμε την πλατεία όπως στην πιο κάτω εικόνα (για  .)
.)![\begin{tikzpicture}[line cap=round,line join=round,>=triangle 45,x=1.0cm,y=1.0cm]
\clip(-0.52,-0.46) rectangle (6.44,4.44);
\fill[fill=black,fill opacity=1.0] (0.,4.) -- (0.,3.) -- (1.,3.) -- (1.,4.) -- cycle;
\fill[fill=black,fill opacity=1.0] (2.,4.) -- (2.,3.) -- (3.,3.) -- (3.,4.) -- cycle;
\fill[fill=black,fill opacity=1.0] (4.,4.) -- (4.,3.) -- (5.,3.) -- (5.,4.) -- cycle;
\fill[fill=black,fill opacity=1.0] (5.,3.) -- (5.,2.) -- (6.,2.) -- (6.,3.) -- cycle;
\fill[fill=black,fill opacity=1.0] (0.,2.) -- (0.,1.) -- (1.,1.) -- (1.,2.) -- cycle;
\fill[fill=black,fill opacity=1.0] (2.,2.) -- (2.,1.) -- (3.,1.) -- (3.,2.) -- cycle;
\fill[fill=black,fill opacity=1.0] (3.,1.) -- (3.,0.) -- (4.,0.) -- (4.,1.) -- cycle;
\fill[fill=black,fill opacity=1.0] (5.,1.) -- (5.,0.) -- (6.,0.) -- (6.,1.) -- cycle;
\draw (0.,0.)-- (0.,4.);
\draw (0.,4.)-- (6.,4.);
\draw (6.,4.)-- (6.,0.);
\draw (6.,0.)-- (0.,0.);
\draw (0.,3.)-- (6.,3.);
\draw (0.,2.)-- (6.,2.);
\draw (0.,1.)-- (6.,1.);
\draw (1.,4.)-- (1.,0.);
\draw (2.,0.)-- (2.,4.);
\draw (3.,4.)-- (3.,0.);
\draw (4.,0.)-- (4.,4.);
\draw (5.,4.)-- (5.,0.);
\draw (0.,4.)-- (0.,3.);
\draw (0.,3.)-- (1.,3.);
\draw (1.,3.)-- (1.,4.);
\draw (1.,4.)-- (0.,4.);
\draw (2.,4.)-- (2.,3.);
\draw (2.,3.)-- (3.,3.);
\draw (3.,3.)-- (3.,4.);
\draw (3.,4.)-- (2.,4.);
\draw (4.,4.)-- (4.,3.);
\draw (4.,3.)-- (5.,3.);
\draw (5.,3.)-- (5.,4.);
\draw (5.,4.)-- (4.,4.);
\draw (5.,3.)-- (5.,2.);
\draw (5.,2.)-- (6.,2.);
\draw (6.,2.)-- (6.,3.);
\draw (6.,3.)-- (5.,3.);
\draw (0.,2.)-- (0.,1.);
\draw (0.,1.)-- (1.,1.);
\draw (1.,1.)-- (1.,2.);
\draw (1.,2.)-- (0.,2.);
\draw (2.,2.)-- (2.,1.);
\draw (2.,1.)-- (3.,1.);
\draw (3.,1.)-- (3.,2.);
\draw (3.,2.)-- (2.,2.);
\draw (3.,1.)-- (3.,0.);
\draw (3.,0.)-- (4.,0.);
\draw (4.,0.)-- (4.,1.);
\draw (4.,1.)-- (3.,1.);
\draw (5.,1.)-- (5.,0.);
\draw (5.,0.)-- (6.,0.);
\draw (6.,0.)-- (6.,1.);
\draw (6.,1.)-- (5.,1.);
\end{tikzpicture} \begin{tikzpicture}[line cap=round,line join=round,>=triangle 45,x=1.0cm,y=1.0cm]
\clip(-0.52,-0.46) rectangle (6.44,4.44);
\fill[fill=black,fill opacity=1.0] (0.,4.) -- (0.,3.) -- (1.,3.) -- (1.,4.) -- cycle;
\fill[fill=black,fill opacity=1.0] (2.,4.) -- (2.,3.) -- (3.,3.) -- (3.,4.) -- cycle;
\fill[fill=black,fill opacity=1.0] (4.,4.) -- (4.,3.) -- (5.,3.) -- (5.,4.) -- cycle;
\fill[fill=black,fill opacity=1.0] (5.,3.) -- (5.,2.) -- (6.,2.) -- (6.,3.) -- cycle;
\fill[fill=black,fill opacity=1.0] (0.,2.) -- (0.,1.) -- (1.,1.) -- (1.,2.) -- cycle;
\fill[fill=black,fill opacity=1.0] (2.,2.) -- (2.,1.) -- (3.,1.) -- (3.,2.) -- cycle;
\fill[fill=black,fill opacity=1.0] (3.,1.) -- (3.,0.) -- (4.,0.) -- (4.,1.) -- cycle;
\fill[fill=black,fill opacity=1.0] (5.,1.) -- (5.,0.) -- (6.,0.) -- (6.,1.) -- cycle;
\draw (0.,0.)-- (0.,4.);
\draw (0.,4.)-- (6.,4.);
\draw (6.,4.)-- (6.,0.);
\draw (6.,0.)-- (0.,0.);
\draw (0.,3.)-- (6.,3.);
\draw (0.,2.)-- (6.,2.);
\draw (0.,1.)-- (6.,1.);
\draw (1.,4.)-- (1.,0.);
\draw (2.,0.)-- (2.,4.);
\draw (3.,4.)-- (3.,0.);
\draw (4.,0.)-- (4.,4.);
\draw (5.,4.)-- (5.,0.);
\draw (0.,4.)-- (0.,3.);
\draw (0.,3.)-- (1.,3.);
\draw (1.,3.)-- (1.,4.);
\draw (1.,4.)-- (0.,4.);
\draw (2.,4.)-- (2.,3.);
\draw (2.,3.)-- (3.,3.);
\draw (3.,3.)-- (3.,4.);
\draw (3.,4.)-- (2.,4.);
\draw (4.,4.)-- (4.,3.);
\draw (4.,3.)-- (5.,3.);
\draw (5.,3.)-- (5.,4.);
\draw (5.,4.)-- (4.,4.);
\draw (5.,3.)-- (5.,2.);
\draw (5.,2.)-- (6.,2.);
\draw (6.,2.)-- (6.,3.);
\draw (6.,3.)-- (5.,3.);
\draw (0.,2.)-- (0.,1.);
\draw (0.,1.)-- (1.,1.);
\draw (1.,1.)-- (1.,2.);
\draw (1.,2.)-- (0.,2.);
\draw (2.,2.)-- (2.,1.);
\draw (2.,1.)-- (3.,1.);
\draw (3.,1.)-- (3.,2.);
\draw (3.,2.)-- (2.,2.);
\draw (3.,1.)-- (3.,0.);
\draw (3.,0.)-- (4.,0.);
\draw (4.,0.)-- (4.,1.);
\draw (4.,1.)-- (3.,1.);
\draw (5.,1.)-- (5.,0.);
\draw (5.,0.)-- (6.,0.);
\draw (6.,0.)-- (6.,1.);
\draw (6.,1.)-- (5.,1.);
\end{tikzpicture}](/forum/ext/geomar/texintegr/latexrender/pictures/102dda3d072c1deca91ec59d57018584.png)
 με
με  .
. 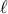 τετράγωνα μαύρα εναλλάξ ξεκινώντας από αριστερά.
τετράγωνα μαύρα εναλλάξ ξεκινώντας από αριστερά. τετράγωνα μαύρα εναλλάξ ξεκινώντας από αριστερά.
τετράγωνα μαύρα εναλλάξ ξεκινώντας από αριστερά. σειρά χρωματίζουμε
σειρά χρωματίζουμε  τετράγωνα μαύρα εναλλάξ ξεκινώντας από αριστερά.
τετράγωνα μαύρα εναλλάξ ξεκινώντας από αριστερά. τετράγωνο μαύρο ξεκινώντας από δεξιά.
τετράγωνο μαύρο ξεκινώντας από δεξιά. σειρά χρωματίζουμε
σειρά χρωματίζουμε  τετράγωνα μαύρα ξεκινώντας από δεξιά.
τετράγωνα μαύρα ξεκινώντας από δεξιά. μαύρα τετράγωνα. Κάθε ένα θέλει από
μαύρα τετράγωνα. Κάθε ένα θέλει από  . Συνολικά λοιπόν χρειάζονται
. Συνολικά λοιπόν χρειάζονται  φανάρια. Πάλι η τοποθέτηση του Διονύση χρησιμοποιεί μόνο τόσο φανάρια.
φανάρια. Πάλι η τοποθέτηση του Διονύση χρησιμοποιεί μόνο τόσο φανάρια.