 θετικός ακέραιος και
θετικός ακέραιος και  ο ελάχιστος ακέραιος τέτοιος ώστε σε οποιουσδήποτε
ο ελάχιστος ακέραιος τέτοιος ώστε σε οποιουσδήποτε  θετικούς ακεραίους να μπορούμε να επιλέξουμε άρτιο πλήθος από αυτούς των οποίων των άθροισμα (των επιλεγέντων) να διαιρείται με το
θετικούς ακεραίους να μπορούμε να επιλέξουμε άρτιο πλήθος από αυτούς των οποίων των άθροισμα (των επιλεγέντων) να διαιρείται με το  Βρείτε το
Βρείτε το 
Συντονιστές: Demetres, socrates, silouan
 θετικός ακέραιος και
θετικός ακέραιος και  ο ελάχιστος ακέραιος τέτοιος ώστε σε οποιουσδήποτε
ο ελάχιστος ακέραιος τέτοιος ώστε σε οποιουσδήποτε  θετικούς ακεραίους να μπορούμε να επιλέξουμε άρτιο πλήθος από αυτούς των οποίων των άθροισμα (των επιλεγέντων) να διαιρείται με το
θετικούς ακεραίους να μπορούμε να επιλέξουμε άρτιο πλήθος από αυτούς των οποίων των άθροισμα (των επιλεγέντων) να διαιρείται με το  Βρείτε το
Βρείτε το 
 τους επιλεγέντες αριθμούς.
τους επιλεγέντες αριθμούς. . Για πλήθος όρων
. Για πλήθος όρων  μπορούμε να επιλέξουμε
μπορούμε να επιλέξουμε  για κάθε
για κάθε  (και το ζητούμενο είναι αδύνατο). Αντίθετα, για πλήθος
(και το ζητούμενο είναι αδύνατο). Αντίθετα, για πλήθος 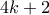 , μεταξύ των
, μεταξύ των  ισοτιμιών των
ισοτιμιών των  θα υπάρχουν τρεις ίδιες (έστω
θα υπάρχουν τρεις ίδιες (έστω  ), οπότε ένα από τα
), οπότε ένα από τα  , που διαιρούνται με το
, που διαιρούνται με το  , θα έχει άρτιο πλήθος όρων. Έτσι,
, θα έχει άρτιο πλήθος όρων. Έτσι, 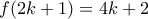 .
. για κάθε
για κάθε  (περιττό ή άρτιο). Πράγματι, για πλήθος
(περιττό ή άρτιο). Πράγματι, για πλήθος  μπορούμε να επιλέξουμε όλους τους αριθμούς ισότιμους με
μπορούμε να επιλέξουμε όλους τους αριθμούς ισότιμους με  (και το ζητούμενο είναι αδύνατο). Αντίθετα, για πλήθος
(και το ζητούμενο είναι αδύνατο). Αντίθετα, για πλήθος  , μεταξύ των
, μεταξύ των  ισοτιμιών των
ισοτιμιών των 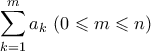 θα υπάρχουν δύο ίδιες (έστω
θα υπάρχουν δύο ίδιες (έστω 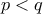 ), οπότε
), οπότε 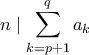 .
. ,
,  αφού μπορούμε να επιλέξουμε
αφού μπορούμε να επιλέξουμε  και
και  για
για  (και το ζητούμενο είναι αδύνατο). Για πλήθος
(και το ζητούμενο είναι αδύνατο). Για πλήθος  , διαχωρίζουμε τα άρτια από τα περιττά
, διαχωρίζουμε τα άρτια από τα περιττά  και, προσθέτοντάς τα ανά δύο, κατασκευάζουμε
και, προσθέτοντάς τα ανά δύο, κατασκευάζουμε  ζεύγη όρων, ξένα μεταξύ τους, όπου το κάθε ζεύγος έχει άρτιο άθροισμα. Έτσι, θεωρώντας τις ισοτιμίες
ζεύγη όρων, ξένα μεταξύ τους, όπου το κάθε ζεύγος έχει άρτιο άθροισμα. Έτσι, θεωρώντας τις ισοτιμίες  των ημιαθροισμάτων σε κάθε ζεύγος, το πρόβλημα ανάγεται στην περίπτωση
των ημιαθροισμάτων σε κάθε ζεύγος, το πρόβλημα ανάγεται στην περίπτωση  χωρίς τον περιορισμό του αρτίου πλήθους (αφού πρόκειται για ζεύγη όρων) η οποία, για πλήθος
χωρίς τον περιορισμό του αρτίου πλήθους (αφού πρόκειται για ζεύγη όρων) η οποία, για πλήθος  , γνωρίζουμε ότι είναι επιλύσιμη. Άρα
, γνωρίζουμε ότι είναι επιλύσιμη. Άρα  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες