 .
. Να βρεθούν όλοι οι φυσικοί
 τέτοιοι ώστε:
τέτοιοι ώστε: 
Συντονιστές: cretanman, silouan, rek2
 .
.  τέτοιοι ώστε:
τέτοιοι ώστε: 
 είναι λύση (αν είναι αποδεκτή). Θα δείξουμε ότι δεν υπάρχουν λύσεις για
είναι λύση (αν είναι αποδεκτή). Θα δείξουμε ότι δεν υπάρχουν λύσεις για  .
.  περιττός, τότε modulo
περιττός, τότε modulo  έχουμε:
έχουμε:
 δεν είναι τέλεια τετράγωνα modulo
δεν είναι τέλεια τετράγωνα modulo  .
.  είναι άρτιος.
είναι άρτιος. τέλειο τετράγωνο, τότε υπάρχει αριθμός
τέλειο τετράγωνο, τότε υπάρχει αριθμός  ελέυθερος τετραγώνου ώστε
ελέυθερος τετραγώνου ώστε  και
και  . Επειδή
. Επειδή  άρτιος, τότε οι
άρτιος, τότε οι  και
και  είναι λύσεις για το
είναι λύσεις για το  στη διοφαντική εξίσωση
στη διοφαντική εξίσωση  .
.  η θεμελιώδης λύση. Τότε έχουμε την αναδρομική σχέση
η θεμελιώδης λύση. Τότε έχουμε την αναδρομική σχέση  με
με  . Αν
. Αν  περιττός, τότε όλα τα
περιττός, τότε όλα τα  είναι περιττοί, άτοπο αφού κάποιο πρέπει να είναι δύναμη του
είναι περιττοί, άτοπο αφού κάποιο πρέπει να είναι δύναμη του  . Άρα
. Άρα  άρτιος. Τότε έχουμε
άρτιος. Τότε έχουμε  άρτιος για κάθε
άρτιος για κάθε  .
. 



 δεν μπορεί να είναι δύναμη του
δεν μπορεί να είναι δύναμη του  . Ούτε όμως το
. Ούτε όμως το  μπορεί να είναι δύναμη του
μπορεί να είναι δύναμη του  αφού είναι και πολλαπλάσιο του
αφού είναι και πολλαπλάσιο του  .
.  .
. !!!
!!! την είχα κάνει ως εξής:
την είχα κάνει ως εξής: αδύνατο.
αδύνατο. τότε
τότε  έχουμε
έχουμε  αδύνατο αρά
αδύνατο αρά 
 τότε
τότε  έχουμε
έχουμε  αδύνατο αρά
αδύνατο αρά 
 τότε
τότε  έχουμε
έχουμε  αδύνατο αρά
αδύνατο αρά 
 .
.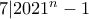 τότε
τότε  άρτιος αδύνατο οπότε θα πρέπει
άρτιος αδύνατο οπότε θα πρέπει  ομως τοτε
ομως τοτε  δινει
δινει αδύνατο.
αδύνατο.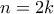 είναι κοινή.
είναι κοινή.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες