Θεωρία αριθμών

2nisic · #1

Παρουσιάζω μία άσκηση που κατασκεύασα:

Κάνοντας χρήση της ανισότητας $(k-1)k^{k-1}< 2^{(k-1)^{2}}$ για κάθε $k\geq 4$
Να προσδιοριστεί το πλήθος τον θετικών ακέραιων λύσεων της εξίσωσης:

$\sum_{i=1}^{k}x_{i}^{k}=n\prod_{i=1}^{k}x_{i}^{k-1}$

Σημείωση:Για k=3

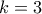και

είναι πρόβλημα που είναι στην περσινή imo shortlist

.
Έχω λύση για την άσκηση αλλά δεν μπορώ να αποδείξω την ανησότητα που απότι βλέπω στο geogebra

ισχύει.

#2

2nisic έγραψε: ↑
Παρ Φεβ 05, 2021 1:38 pm

Κάνοντας χρήση της ανισότητας $(k-1)k^{k-1}< 2^{(k-1)^{2}}$ για κάθε $k\geq 4$
...

δεν μπορώ να αποδείξω την ανησότητα που απότι βλέπω στο ισχύει.

Ας δούμε απόδειξη της ανισότητας, ισοδύναμα της $2^{n^2}> n(n+1)^n$ για $n\ge 3$ .

Πρώτα απ΄όλα επαγωγικά 2^m > 1+2m

για φυσικούς $m\ge 3$ (απόδειξη του επαγωγικού βήματος: $2^{m+1} =2\cdot 2^m\ge 2(1+2m)= 3+2m+(2m-1) >3+2m= 1+2(m+1)$ ).

Έχουμε λοιπόν

$\displaystyle{2^{n^2} = \left (2^{n-1} \right )^n2^n > (1 +2(n-1))^n (1+2n) = (2n-1)^n(1+2n) > (n+1)^n(1+2n) > (n+1)^nn}$ , όπως θέλαμε.

Σχόλιο: Η ανισότητα ισχύει "και με περίσσευμα" καθώς αποδεικνύεται ότι $\displaystyle{\dfrac {2^{n^2}}{n(n+1)^n} \to \infty}$ . Αυτό αιτιολογεί και τις "γεναιόδωρες" ανισώσεις στην παραπάνω απόδειξη.

2nisic · #3

Μια απόδειξη τής ανησοτητας από τον sanyalarnab

It's actually quite easy.
1st thing to do is to take log_2

on both sides of the inequality .After some shuffling of variables,
we'll get $(m-1)(m-1-log_2m)\ge log_2(m-1)$
Clearly $(m-1)\ge log_2(m-1)$ .Again we observe
m=4

leads to

.So , for all $m\ge 4$ ,
$(m-1-log_2m)\ge 1$ .So the original equation turns out to be true for all $m\ge 4$ .Now we check for
m=1,2 ,3

and see that only 3 dissatisfies the equation.

Θεωρία αριθμών

Θεωρία αριθμών

Re: Θεωρία αριθμών

Re: Θεωρία αριθμών

Μέλη σε σύνδεση