 είναι θετικοί ακέραιοι και
είναι θετικοί ακέραιοι και  πρώτος να λυθεί η εξίσωση
πρώτος να λυθεί η εξίσωση
Συντονιστές: cretanman, silouan, rek2
Καλησπέρα.Xriiiiistos έγραψε: ↑Κυρ Ιαν 06, 2019 11:18 pmΑνείναι θετικοί ακέραιοι και
πρώτος να λυθεί η εξίσωση

 θετικοί ακέραιοι με
θετικοί ακέραιοι με  πρώτο και
πρώτο και  . Τότε,
. Τότε,  και
και  .
.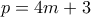 .
. , τότε
, τότε  και τούμπαλιν.
και τούμπαλιν. δεν διαιρείται από το
δεν διαιρείται από το  .
.
 , άτοπο.
, άτοπο. και
και  και η απόδειξη του Λήμματος ολοκληρώθηκε.
και η απόδειξη του Λήμματος ολοκληρώθηκε. , τότε
, τότε  , άρα
, άρα  οπότε προκύπτει
οπότε προκύπτει  .
. .
. .
.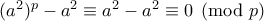 , οπότε η δεδομένη εξίσωση
, οπότε η δεδομένη εξίσωση  δίνει
δίνει  .
. , τότε από το Λήμμα,
, τότε από το Λήμμα,  άτοπο.
άτοπο. και παίρνοντας
και παίρνοντας  την δοσμένη προκύπτει
την δοσμένη προκύπτει  .
. . Αν
. Αν  , τότε
, τότε  , άτοπο.
, άτοπο. , όμοια
, όμοια  , άτοπο.
, άτοπο. .
. δεν υπάρχουν λύσεις. Ούτε επίσης για
δεν υπάρχουν λύσεις. Ούτε επίσης για  . Πρέπει
. Πρέπει 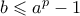 αφού αν
αφού αν  τότε
τότε  . Αφού
. Αφού  , τότε
, τότε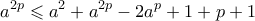
 . Για
. Για  παίρνουμε
παίρνουμε  και αφού
και αφού  τότε
τότε 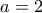 . Αυτό με την σειρά του δίνει
. Αυτό με την σειρά του δίνει  και την λύση
και την λύση  .
. (και
(και  ) έχουμε
) έχουμε
 για
για  . Αυτό όμως είναι άτοπο αφού έχουμε επίσης ότι
. Αυτό όμως είναι άτοπο αφού έχουμε επίσης ότι  .
. .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες