 και ας είναι
και ας είναι 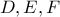 τα σημεία επαφής του έγκυκλου
τα σημεία επαφής του έγκυκλου  του
του  με τις πλευρές
με τις πλευρές  αντίστοιχα και
αντίστοιχα και  το δεύτερο (εκτός του
το δεύτερο (εκτός του  ) σημείου τομής της
) σημείου τομής της  με τον
με τον  . Να δείξετε ότι
. Να δείξετε ότι 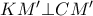 , όπου
, όπου  είναι το συμμετρικό του μέσου
είναι το συμμετρικό του μέσου  του τμήματος
του τμήματος  ως προς την
ως προς την 
Συντονιστές: vittasko, silouan, Doloros
 και ας είναι
και ας είναι 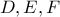 τα σημεία επαφής του έγκυκλου
τα σημεία επαφής του έγκυκλου  του
του  με τις πλευρές
με τις πλευρές  αντίστοιχα και
αντίστοιχα και  το δεύτερο (εκτός του
το δεύτερο (εκτός του  ) σημείου τομής της
) σημείου τομής της  με τον
με τον  . Να δείξετε ότι
. Να δείξετε ότι 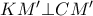 , όπου
, όπου  είναι το συμμετρικό του μέσου
είναι το συμμετρικό του μέσου  του τμήματος
του τμήματος  ως προς την
ως προς την 
 , εγγεγραμμένο σε κύκλο κέντρου
, εγγεγραμμένο σε κύκλο κέντρου  , και έστω
, και έστω  το μέσο της πλευράς
το μέσο της πλευράς  . ΟΙ εφαπτομένες του κύκλου
. ΟΙ εφαπτομένες του κύκλου  στα
στα  ,
,  τέμνονται στο σημείο
τέμνονται στο σημείο  . Αν
. Αν 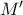 το
το ως προς την
ως προς την  , να αποδείξετε ότι
, να αποδείξετε ότι  .
Δίνουμε και το σχήμα του αρχικού προβλήματος, ώστε να φαίνεται το ταυτόσημο των δύο προβλημάτων. Θα εργαστούμε στο 2ο σχήμα.
.
Δίνουμε και το σχήμα του αρχικού προβλήματος, ώστε να φαίνεται το ταυτόσημο των δύο προβλημάτων. Θα εργαστούμε στο 2ο σχήμα. φέρουμε το ύψος
φέρουμε το ύψος  . Επίσης, στο τρίγωνο αυτό η
. Επίσης, στο τρίγωνο αυτό η  είναι η ευθεία της
είναι η ευθεία της , η
, η 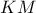 διάμεσος, και
διάμεσος, και  ακτίνα του περιγεγραμμένου κύκλου του.
ακτίνα του περιγεγραμμένου κύκλου του.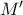 ,
,  είναι τα συμμετρικά του
είναι τα συμμετρικά του  ως προς τις πλευρές
ως προς τις πλευρές  ,
,  του τριγώνου
του τριγώνου  αντίστοιχα. Έστω επίσης
αντίστοιχα. Έστω επίσης  .
. (γνωστή ιδιότητα της συμμετροδιαμέσου - διαμέσου).
(γνωστή ιδιότητα της συμμετροδιαμέσου - διαμέσου).  είναι εγγράψιμο, οπότε
είναι εγγράψιμο, οπότε  ,
,  .
Θα αποδείξουμε ότι τα τρίγωνα
.
Θα αποδείξουμε ότι τα τρίγωνα  και
και  είναι όμοια.
είναι όμοια. με την ακτίνα
με την ακτίνα  , όπως και η διάμεσος
, όπως και η διάμεσος 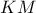 με τη
με τη  , είναι ευθείες ισογώνιες ως προς τις πλευρές της γωνίας
, είναι ευθείες ισογώνιες ως προς τις πλευρές της γωνίας  .
. . Αλλά,
. Αλλά,  (εντός εναλλάξ)
(εντός εναλλάξ) , και εφόσον έχουν κοινή τη γωνία
, και εφόσον έχουν κοινή τη γωνία 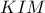 ,
, .
. . Πράγματι,
. Πράγματι,  .
.
 . Από τις δύο αυτές ισότητες προκύπτει ότι
. Από τις δύο αυτές ισότητες προκύπτει ότι  .
. και
και 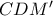 είναι όμοια.
είναι όμοια.
 (εφόσον
(εφόσον  και
και  ).
). και
και  .
. και
και 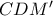 είναι όμοια, οπότε
είναι όμοια, οπότε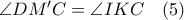 και
και 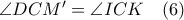 .
. .
. είναι εγγράψιμο, και ως εκ τούτου
είναι εγγράψιμο, και ως εκ τούτου . Από (1) και (7) έχουμε
. Από (1) και (7) έχουμε  (λόγω και της (5)).
(λόγω και της (5)). , τότε
, τότε  , οπότε
, οπότε  , και λόγω της (4)
, και λόγω της (4)  ,
, 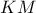 εφάπτεται του περιγεγραμμένου κύκλου του τετραπλεύρου
εφάπτεται του περιγεγραμμένου κύκλου του τετραπλεύρου  .
.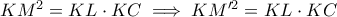 , από την οποία προκύπτει ότι το τρίγωνο
, από την οποία προκύπτει ότι το τρίγωνο 
 .
.Νομίζω πως είναι απλό για τον φάκελο, στην πραγματικότητα το μισό σχήμα είναι παραπλανητικό:ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ έγραψε: ↑Παρ Νοέμ 19, 2021 11:38 amΔύο κάθετες.png
Έστω τρίγωνοκαι ας είναι
τα σημεία επαφής του έγκυκλου
του
με τις πλευρές
αντίστοιχα και
το δεύτερο (εκτός του
) σημείου τομής της
με τον
. Να δείξετε ότι
, όπου
είναι το συμμετρικό του μέσου
του τμήματος
ως προς την

 ύψος στο
ύψος στο 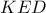 . Τότε
. Τότε  και επίσης
και επίσης  (αφού
(αφού  παραλληλόγραμμο ) .
παραλληλόγραμμο ) .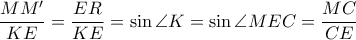 έτσι
έτσι  όμοια. Τώρα
όμοια. Τώρα  (
( συμμετροδιάμεσος)
συμμετροδιάμεσος) πάνω στην
πάνω στην  . Το ότι βρίσκουμε μια σύντομη λύση δεν κάνει το πρόβλημα απλό. Άλλωστε η μαγεία της Γεωμετρίας έγκειται ακριβώς εκεί, δηλαδή να ανακαλύψει μία βοηθητική γραμμή.
. Το ότι βρίσκουμε μια σύντομη λύση δεν κάνει το πρόβλημα απλό. Άλλωστε η μαγεία της Γεωμετρίας έγκειται ακριβώς εκεί, δηλαδή να ανακαλύψει μία βοηθητική γραμμή. λόγω της ισότητας
λόγω της ισότητας  προκύπτει η ομοιότητα
προκύπτει η ομοιότητα  καθώς
καθώς  , ενώ οι πλευρές
, ενώ οι πλευρές  είναι κάθετες προς τις
είναι κάθετες προς τις  αντίστοιχα.
αντίστοιχα.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης