Πρόκειται για το πρόβλημα 2052 του Mathematics Magazine, που προτάθηκε τον Οκτώβριο 2018 από τον
Michel Bataillle, με λύση στο τ. 4, σελ. 313, τον Οκτώβριο, 2019.
Ακολουθεί η λύση που είχα στείλει:
Λύση: Παρατηρούμε ότι

, οπότε τα ισοσκελή τρίγωνα

,

είναι όμοια με λόγο ομοιότητας ίσο με

, ενώ οι πλευρές του

είναι παράλληλες στις πλευρές του

Επίσης, τα τρίγωνα

και

έχουν το ίδιο ύψος από το

στην

, οπότε

Αφού

, εάν ήταν

, τότε το

θα ήταν όμοιο με το τρίγωνο

με

. Όμως, αυτό δεν μπορεί να ισχύει ανεξάρτητα από το που βρίσκεται το

στην ευθεία

με

επειδή το τρίγωνο

είναι σκαληνό. Επομένως

και οι ευθείες

και

τέμνονται σε ένα σημείο, έστω το

. Το

είναι το κέντρο ομοιοθεσίας με λόγο

που απεικονίζει το

στο

οπότε

Επιπλέον, είναι

και έτσι

αφού τα τρίγωνα

και

έχουν το ίδιο ύψος από το

προς την

, και

. Πολ/ντας τις (1) και (2) παίρνουμε

Συνεπώς, το

είναι ένα σημείο ανεξάρτητο της επιλογής το

και η απόδειξη μας είναι πλήρης.
Σχόλιο: Έστω ότι η
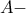
συμμετροδιάμεσος του

τέμνει την

στο

. Είναι γνωστό ότι

οπότε, από την τελευταία ισότητα αποδεικνύει ότι το

είναι το αρμονικό συζυγές του

ως προς το

και το

.
 ένα σκαληνό τρίγωνο. Έστω
ένα σκαληνό τρίγωνο. Έστω  ένα μεταβλητό σημείο στην ευθεία
ένα μεταβλητό σημείο στην ευθεία  τέτοιο ώστε
τέτοιο ώστε  και
και  . Έστω σημείο
. Έστω σημείο  στην
στην  ώστε η
ώστε η  να είναι η ανάκλαση της
να είναι η ανάκλαση της  ως προς την διχοτόμο της γωνίας
ως προς την διχοτόμο της γωνίας  . Έστω
. Έστω  ,
,  τα περίκεντρα των τριγώνων
τα περίκεντρα των τριγώνων  and
and  , αντίστοιχα. Να δειχθεί ότι υπάρχει ένα σημείο
, αντίστοιχα. Να δειχθεί ότι υπάρχει ένα σημείο  , ανεξάρτητο από την επιλογή του
, ανεξάρτητο από την επιλογή του  , τέτοιο ώστε η ευθεία
, τέτοιο ώστε η ευθεία  να διέρχεται από το
να διέρχεται από το 

 . Έτσι έχω την προβολική σύνδεση
. Έτσι έχω την προβολική σύνδεση  .
. μέσον του
μέσον του  και
και  μέσον του
μέσον του  .
. και
και  είναι προβολικότητες. Το
είναι προβολικότητες. Το  . Έτσι
. Έτσι  προβολικότητα . Όμοια
προβολικότητα . Όμοια  προβολικότητα.
προβολικότητα. με τα
με τα  να κινούνται σε σταθερές ευθείες. Είναι απλό ότι όταν το ένα γίνει περίκεντρο γίνεται και το άλλο, κατά τα γνωστά λοιπόν η
να κινούνται σε σταθερές ευθείες. Είναι απλό ότι όταν το ένα γίνει περίκεντρο γίνεται και το άλλο, κατά τα γνωστά λοιπόν η  διέρχεται από σταθερό σημείο, το οποίο δεν χρειάστηκε καν να βρούμε....η δύναμη της προβολικής
διέρχεται από σταθερό σημείο, το οποίο δεν χρειάστηκε καν να βρούμε....η δύναμη της προβολικής  .
. στο σημείο
στο σημείο  .
. και το
και το  είναι εγγεγραμμένο σε κύκλο έχουμε ότι
είναι εγγεγραμμένο σε κύκλο έχουμε ότι  και
και  .
. και
και  είναι όμοια και έχουν τις πλευρές τους παράλληλες οπότε είναι ομοιόθετα και το κέντρο της ομοιοθεσίας,έστω
είναι όμοια και έχουν τις πλευρές τους παράλληλες οπότε είναι ομοιόθετα και το κέντρο της ομοιοθεσίας,έστω  και
και  δηλαδή η
δηλαδή η  εφάπτεται στον περίκυκλο του τριγώνου
εφάπτεται στον περίκυκλο του τριγώνου  και άρα το
και άρα το  είναι τα ομοιόθετα των
είναι τα ομοιόθετα των  και
και  και άρα η
και άρα η 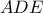 το οποίο αποδεικνύει το ζητούμενο και στην περίπτωση που το
το οποίο αποδεικνύει το ζητούμενο και στην περίπτωση που το  και
και  .
. , οπότε τα ισοσκελή τρίγωνα
, οπότε τα ισοσκελή τρίγωνα  ,
,  είναι όμοια με λόγο ομοιότητας ίσο με
είναι όμοια με λόγο ομοιότητας ίσο με  , ενώ οι πλευρές του
, ενώ οι πλευρές του  Επίσης, τα τρίγωνα
Επίσης, τα τρίγωνα  και
και  έχουν το ίδιο ύψος από το
έχουν το ίδιο ύψος από το  στην
στην 
 , εάν ήταν
, εάν ήταν  , τότε το
, τότε το  θα ήταν όμοιο με το τρίγωνο
θα ήταν όμοιο με το τρίγωνο  με
με  . Όμως, αυτό δεν μπορεί να ισχύει ανεξάρτητα από το που βρίσκεται το
. Όμως, αυτό δεν μπορεί να ισχύει ανεξάρτητα από το που βρίσκεται το  επειδή το τρίγωνο
επειδή το τρίγωνο  και οι ευθείες
και οι ευθείες  που απεικονίζει το
που απεικονίζει το  οπότε
οπότε
 και έτσι
και έτσι
 έχουν το ίδιο ύψος από το
έχουν το ίδιο ύψος από το  . Πολ/ντας τις (1) και (2) παίρνουμε
. Πολ/ντας τις (1) και (2) παίρνουμε 
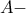 συμμετροδιάμεσος του
συμμετροδιάμεσος του  στο
στο  . Είναι γνωστό ότι
. Είναι γνωστό ότι  οπότε, από την τελευταία ισότητα αποδεικνύει ότι το
οπότε, από την τελευταία ισότητα αποδεικνύει ότι το