ΚΕΦΑΛΟΝΙΤΗΣ έγραψε: ↑Κυρ Μαρ 28, 2021 11:28 am
Τις τελευταίες μέρες με απασχόλησαν κάποιες σκέψεις που με οδήγησαν στο παρακάτω θέμα.
Κατανοώ ότι αρκετοί μόλις το δουν θα προχωρήσουν σε κάτι άλλο, η Στερεομετρία δεν είναι της μόδας...
Το δημοσιεύω γιατί πιστεύω ότι κάτι αξίζει...
Άλλωστε τα μαθηματικά δεν χάνουν την αξία τους, μπορεί κάποια θέματα να είναι εκτός σχολικής εξέτασης αλλά εξακολουθούν να είναι πολύτιμα.
Σαν το παλιό κρασί που μένει για πολλά χρόνια σε κάποιο βαρέλι, αυτός που θα το δοκιμάσει θα το απολαύσει πολύ...
Δίνεται κύκλος κέντρου

και ακτίνας

Έστω
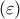
ο η εφαπτομένη του κύκλου στο σταθερό σημείο του

Να ορισθεί η θέση της διαμέτρου

έτσι ώστε αν σχεδιαστούν οι

κάθετοι στην
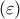
, η ολική επιφάνεια του κόλουρου κώνου που γράφεται από το τραπέζιο

στρεφόμενο περί την
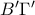
να είναι ίση με
 ΜΕΤΑΓΕΝΕΣΤΕΡΗ ΔΙΕΥΚΡΙΝΗΣΗ
To να ζητήσω η ολική επιφάνεια του κόλουρου κώνου να είναι ίση με
ΜΕΤΑΓΕΝΕΣΤΕΡΗ ΔΙΕΥΚΡΙΝΗΣΗ
To να ζητήσω η ολική επιφάνεια του κόλουρου κώνου να είναι ίση με  ήταν μια ατυχής και λανθασμένη απόφαση. Αυτό φαίνεται από τη λύση του Νίκου Μαυρογιάννη. To σωστό θα ήταν να γράψω
ήταν μια ατυχής και λανθασμένη απόφαση. Αυτό φαίνεται από τη λύση του Νίκου Μαυρογιάννη. To σωστό θα ήταν να γράψω 
Τηλέμαχε και Νίκο καλημέρα και καλό μήνα...
Μετά τη διευκρίνηση του Τηλέμαχου αναρτώ και μια άλλη διαπραγμάτευση με τη βοήθεια του τριωνύμου.
Εργαζόμαστε στο ακόλουθο σχήμα:

- Κόλουρος κώνος 1.png (11.67 KiB) Προβλήθηκε 637 φορές
Η περιστροφή της διαμέτρου

γύρω από τον άξονα των

κατά γωνία ίση με

είναι
η κυρτή επιφάνεια ενός κόλουρου κώνου, όπως φαίνεται στο ακόλουθο σχήμα:

- Κόλουρος κώνος 5.png (45.77 KiB) Προβλήθηκε 637 φορές
Η κυρτή επιφάνεια του κόλουρου αυτού κώνου είναι ίση με

και αν σ' αυτήν προστεθούν τα εμβαδά
των δύο βάσεων τότε η ολική του επιφάνεια θα είναι:

όπου:

και για τα τμήματα αυτά προφανώς ισχύει:

Στο πρόβλημα αυτό μας ζητάει να ισχύει:

Από τις (1) και (2) προκύπτει:

ή μετά πράξεις και με τη βοήθεια της (2), θα είναι:

Οι εξισώσεις (1) και (4) μα οδηγούν στη λύση του τριωνύμου της μορφής:

δηλαδή του τριωνύμου:

Για να έχει η εξίσωση αυτή δυο ρίζες πραγματικές και μάλιστα μη αρνητικές θα πρέπει:

Από τις συνθήκες (6) προκύπτει:

και

Άρα για το συντελεστή

πρέπει να ισχύει:

Αν

τότε ο κόλουρος κώνος γίνεται κύλινδρος με ακτίνα βάσης

και ύψος

.
Αν

τότε ο κόλουρος κώνος γίνεται κύκλος με ακτίνα ίση με

Οι οριακές περιπτώσεις φαίνονται στα παρακάτω σχήματα:
Για


- Κόλουρος κώνος 3.png (52.82 KiB) Προβλήθηκε 637 φορές
Για


- Κόλουρος κώνος 4.png (68.19 KiB) Προβλήθηκε 637 φορές
Κώστας Δόρτσιος
 και ακτίνας
και ακτίνας  Έστω
Έστω 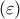 ο η εφαπτομένη του κύκλου στο σταθερό σημείο του
ο η εφαπτομένη του κύκλου στο σταθερό σημείο του  Να ορισθεί η θέση της διαμέτρου
Να ορισθεί η θέση της διαμέτρου  έτσι ώστε αν σχεδιαστούν οι
έτσι ώστε αν σχεδιαστούν οι  κάθετοι στην
κάθετοι στην 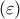 , η ολική επιφάνεια του κόλουρου κώνου που γράφεται από το τραπέζιο
, η ολική επιφάνεια του κόλουρου κώνου που γράφεται από το τραπέζιο  στρεφόμενο περί την
στρεφόμενο περί την 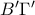 να είναι ίση με
να είναι ίση με 
 ήταν μια ατυχής και λανθασμένη απόφαση. Αυτό φαίνεται από τη λύση του Νίκου Μαυρογιάννη. To σωστό θα ήταν να γράψω
ήταν μια ατυχής και λανθασμένη απόφαση. Αυτό φαίνεται από τη λύση του Νίκου Μαυρογιάννη. To σωστό θα ήταν να γράψω 

 που σχηματίζει η διάμετρος με την εφαπτομένη.
που σχηματίζει η διάμετρος με την εφαπτομένη.  και
και 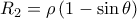 και πλευρά
και πλευρά  . Η επιφάνεια του θα είναι:
. Η επιφάνεια του θα είναι: 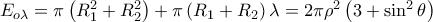 .
. και πρέπει
και πρέπει  .
.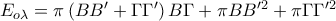
 η
η 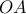 είναι διάμεσος, άρα
είναι διάμεσος, άρα 

![4\pi \rho ^{2}+\pi \left [ \left ( BB'+\Gamma \Gamma ' \right )^{2} -2BB'\cdot \Gamma \Gamma '\right ]= 4\pi \rho ^{2}+\pi \left [ \left ( BB'+\Gamma \Gamma ' \right )^{2} -2BB'\cdot \Gamma \Gamma '\right ]=](/forum/ext/geomar/texintegr/latexrender/pictures/45046f462c261cd1f32902ceba1110f1.png)
![4\pi \rho ^{2}+\pi \left [ \left ( 2\rho \right )^{2}-2BB'\cdot \Gamma \Gamma '\right ]= 4\pi \rho ^{2}+\pi \left [ \left ( 2\rho \right )^{2}-2BB'\cdot \Gamma \Gamma '\right ]=](/forum/ext/geomar/texintegr/latexrender/pictures/ade9c7ba88a01275b8f13509b39a4559.png)
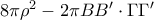
 βρίσκεται ότι
βρίσκεται ότι 









 προκύπτει αν σκεφτούμε ότι
προκύπτει αν σκεφτούμε ότι 

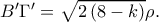
 έτσι ώστε
έτσι ώστε 
 . Βρίσκω το αντιδιαμετρικό του
. Βρίσκω το αντιδιαμετρικό του 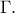
 είναι η ζητουμένη διάμετρος.
είναι η ζητουμένη διάμετρος. γύρω από τον άξονα των
γύρω από τον άξονα των  κατά γωνία ίση με
κατά γωνία ίση με  είναι
είναι  και αν σ' αυτήν προστεθούν τα εμβαδά
και αν σ' αυτήν προστεθούν τα εμβαδά 










 πρέπει να ισχύει:
πρέπει να ισχύει: 
 τότε ο κόλουρος κώνος γίνεται κύλινδρος με ακτίνα βάσης
τότε ο κόλουρος κώνος γίνεται κύλινδρος με ακτίνα βάσης  και ύψος
και ύψος  .
. τότε ο κόλουρος κώνος γίνεται κύκλος με ακτίνα ίση με
τότε ο κόλουρος κώνος γίνεται κύκλος με ακτίνα ίση με