Δίνεται ένα κυρτό τετράπλευρο
 και οι διαγώνιες του
και οι διαγώνιες του  που τέμνονται στο
που τέμνονται στο  . Θεωρούμε τα ορθόκεντρα
. Θεωρούμε τα ορθόκεντρα  των τριγώνων
των τριγώνων  και
και  αντίστοιχα και τα βαρύκεντρα
αντίστοιχα και τα βαρύκεντρα  των τριγώνων
των τριγώνων και
και  αντίστοιχα. Να αποδείξετε ότι το τμήμα
αντίστοιχα. Να αποδείξετε ότι το τμήμα  είναι κάθετο στο
είναι κάθετο στο 
Συντονιστές: vittasko, silouan, Doloros
 και οι διαγώνιες του
και οι διαγώνιες του  που τέμνονται στο
που τέμνονται στο  . Θεωρούμε τα ορθόκεντρα
. Θεωρούμε τα ορθόκεντρα  των τριγώνων
των τριγώνων  και
και  αντίστοιχα και τα βαρύκεντρα
αντίστοιχα και τα βαρύκεντρα  των τριγώνων
των τριγώνων και
και  αντίστοιχα. Να αποδείξετε ότι το τμήμα
αντίστοιχα. Να αποδείξετε ότι το τμήμα  είναι κάθετο στο
είναι κάθετο στο 
Καλησπέρα Άρχοντα ΣωτήρηS.E.Louridas έγραψε: ↑Δευ Μαρ 08, 2021 8:00 pmΕπιτρέψτε μου να προτείνω ένα πρόβλημα από το διαδύκτιο, που εισηγήθηκε ο Άριστος συνάδελφος Σωτήρης Γκουντουβάς, και που μου άρεσε πολύ.
Δίνεται ένα κυρτό τετράπλευροκαι οι διαγώνιες του
που τέμνονται στο
. Θεωρούμε τα ορθόκεντρα
των τριγώνων
και
αντίστοιχα και τα βαρύκεντρα
των τριγώνων
και
αντίστοιχα. Να αποδείξετε ότι το τμήμα
είναι κάθετο στο
 (από Θαλή) , όπου
(από Θαλή) , όπου  τα μέσα των
τα μέσα των  αντίστοιχα.
αντίστοιχα.  το συμμετρικό του
το συμμετρικό του  ως προς το
ως προς το  , τότε από το παραλληλόγραμμο
, τότε από το παραλληλόγραμμο  (οι διαγώνιες διχοτομούνται) , θα είναι
(οι διαγώνιες διχοτομούνται) , θα είναι  , και από το τρίγωνο
, και από το τρίγωνο 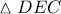 θα είναι
θα είναι 
 .
. ισχύουν οι προϋποθέσεις της πρότασή σου αυτής (λόγω των ίσων κατακορυφήν γωνιών του ) και συνεπώς θα είναι
ισχύουν οι προϋποθέσεις της πρότασή σου αυτής (λόγω των ίσων κατακορυφήν γωνιών του ) και συνεπώς θα είναι  . Από την προκύπτει ότι τα τρίγωνα
. Από την προκύπτει ότι τα τρίγωνα  και
και  είναι όμοια (δύο πλευρές ανάλογες και τις περιεχόμενες γωνίες τους ίσες (κάθετες πλευρές του ίδιου προσανατολισμού)) και συνεπώς θα είναι και
είναι όμοια (δύο πλευρές ανάλογες και τις περιεχόμενες γωνίες τους ίσες (κάθετες πλευρές του ίδιου προσανατολισμού)) και συνεπώς θα είναι και  και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί.Καταρχάς Στάθη ευχαριστώ πάρα πολύ για την άριστη διαπραγμάτευση σου.ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ έγραψε: ↑Τρί Μαρ 09, 2021 5:26 pmΚαλησπέρα Άρχοντα ΣωτήρηS.E.Louridas έγραψε: ↑Δευ Μαρ 08, 2021 8:00 pmΕπιτρέψτε μου να προτείνω ένα πρόβλημα από το διαδύκτιο, που εισηγήθηκε ο Άριστος συνάδελφος Σωτήρης Γκουντουβάς, και που μου άρεσε πολύ.
Δίνεται ένα κυρτό τετράπλευροκαι οι διαγώνιες του
που τέμνονται στο
. Θεωρούμε τα ορθόκεντρα
των τριγώνων
και
αντίστοιχα και τα βαρύκεντρα
των τριγώνων
και
αντίστοιχα. Να αποδείξετε ότι το τμήμα
είναι κάθετο στο
Η πλάκα είναι ότι το συγκεκριμένο πρόβλημα μας το έχεις λύσει και εδώ στο Mathematica ! και ας λες ότι δεν το λύνεις για να το δοκιμάσουμε.
Πιστεύω ότι δεν έχεις διαφορετική λύση αφού εσύ έβαλες το Λήμμα που το λύνει. Δεν το γνωρίζω, ίδωμεν
Sotiris Louridas.png
Προφανώς(από Θαλή) , όπου
τα μέσα των
αντίστοιχα.
Αντο συμμετρικό του
ως προς το
, τότε από το παραλληλόγραμμο
(οι διαγώνιες διχοτομούνται) , θα είναι
, και από το τρίγωνο
θα είναι
Με.
Για τα τρίγωναισχύουν οι προϋποθέσεις της πρότασή σου αυτής (λόγω των ίσων κατακορυφήν γωνιών του ) και συνεπώς θα είναι
. Από την προκύπτει ότι τα τρίγωνα
και
είναι όμοια (δύο πλευρές ανάλογες και τις περιεχόμενες γωνίες τους ίσες (κάθετες πλευρές του ίδιου προσανατολισμού)) και συνεπώς θα είναι και
και το ζητούμενο έχει αποδειχθεί.
Με όλη μου την εκτίμηση
Στάθης
 με
με  και
και 
 μέσο της
μέσο της  , άρα από την προκύπτουσα ομοιότητα των τριγώνων
, άρα από την προκύπτουσα ομοιότητα των τριγώνων  άμεσα έχουμε:
άμεσα έχουμε: 
 (*) Εδώ μπορούμε να δούμε το ιστορικό της Άσκησης αυτής: https://www.facebook.com/groups/1664980577160670
(*) Εδώ μπορούμε να δούμε το ιστορικό της Άσκησης αυτής: https://www.facebook.com/groups/1664980577160670 και σημεία
και σημεία  ,
,  των
των  ,
,  με
με  ,
,  . Αν οι
. Αν οι  τέμνονται στο
τέμνονται στο  να εκφραστεί το
να εκφραστεί το  ως γραμμικός συνδυασμός των
ως γραμμικός συνδυασμός των  ,
,  .
Για ευκολία γράφουμε
.
Για ευκολία γράφουμε  και από τις σχέσεις
και από τις σχέσεις  (*)
(*) και επομένως το σύστημα
και επομένως το σύστημα  . Από αυτό βρίσκουμε ότι
. Από αυτό βρίσκουμε ότι  . Αντικαθιστώντας σε κάποια από τις (*) καταλήγουμε στην
. Αντικαθιστώντας σε κάποια από τις (*) καταλήγουμε στην  .
. και
και  . Οι συντελεστές
. Οι συντελεστές  για την περίπτωση των βαρυκέντρων είναι όλοι ίσοι με
για την περίπτωση των βαρυκέντρων είναι όλοι ίσοι με  ενώ στην περίπτωση των ορθοκέντρων προκύπτουν από το ότι η προβολή του τυχόντος
ενώ στην περίπτωση των ορθοκέντρων προκύπτουν από το ότι η προβολή του τυχόντος  στο τυχόν
στο τυχόν  είναι ίση με
είναι ίση με  .
Έτσι με
.
Έτσι με  έχουμε:
έχουμε:
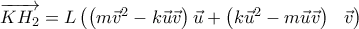
![\overrightarrow{H_{1}H_{2}}=L\left[ \left( k-1\right) \overset{\vec{\sigma}}{\overbrace{\left( \vec{u}^{2}\ \vec{v}-\left( \vec{u}\vec{v}\right) \vec{u}\right) }}+\left( m-1\right) \overset{\vec{\tau}}{\overbrace{\left( \ \vec{v}^{2}\vec{u}-\left( \vec{u}\vec{v}\right) \ \vec{v}\right) }}\right] \overrightarrow{H_{1}H_{2}}=L\left[ \left( k-1\right) \overset{\vec{\sigma}}{\overbrace{\left( \vec{u}^{2}\ \vec{v}-\left( \vec{u}\vec{v}\right) \vec{u}\right) }}+\left( m-1\right) \overset{\vec{\tau}}{\overbrace{\left( \ \vec{v}^{2}\vec{u}-\left( \vec{u}\vec{v}\right) \ \vec{v}\right) }}\right]](/forum/ext/geomar/texintegr/latexrender/pictures/a399ed3166b760cddb43bc65982c7126.png)



 και επομένως
και επομένως 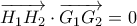 και η ζητούμενη καθετότητα έπεται.
και η ζητούμενη καθετότητα έπεται.  και
και  στην 7η γραμμή.
στην 7η γραμμή.Καταρχάς και κυρίως Καταρχήν Νίκο σε ευχαριστώ που ασχολήθηκες με Άριστο, κατά την άποψη μου, τρόπο με θέμα που επέλεξα να προτείνω.nsmavrogiannis έγραψε: ↑Πέμ Μαρ 11, 2021 1:50 amΓεια σας
Υπό άλλες περιστάσεις δεν θα έγραφα την παρακάτω λύση με διανύσματα μιας και έχουμε ήδη δύο ωραίες λύσεις με συνθετική Γεωμετρία από τον Στάθη και τον Σωτήρη. Ο λόγος που το κάνω έχει να κάνει με κάποια σχόλια που θα ακολουθήσουν.
Κατ΄αρχάς παραθέτω ένα κοινόχρηστο αποτέλεσμα που υπάρχει εδώ και εκεί και ίσως κάπου στο. Όταν δίδασκα διανύσματα στην Α΄Δέσμη ή στην Κατεύθυνση της Β΄Λυκείου (ακόμα και με το πετσοκομένο δίωρο) δεν παρέλειπα να το διδάσκω:
Έστω τρίγωνοκαι σημεία
,
των
,
με
,
. Αν οι
τέμνονται στο
να εκφραστεί το
ως γραμμικός συνδυασμός των
,
.
H-G1.png
Για ευκολία γράφουμεκαι από τις σχέσεις
(*)
έχουμe τηνκαι επομένως το σύστημα
. Από αυτό βρίσκουμε ότι
. Αντικαθιστώντας σε κάποια από τις (*) καταλήγουμε στην
.
Μπορούμε τώρα να εφαρμόσουμε την παραπάνω σχέση σε κάθε ένα από τα τέσσερα τρίγωνα του τετραπλεύρου θέτονταςκαι
. Οι συντελεστές
για την περίπτωση των βαρυκέντρων είναι όλοι ίσοι με
ενώ στην περίπτωση των ορθοκέντρων προκύπτουν από το ότι η προβολή του τυχόντος
στο τυχόν
είναι ίση με
.
H-G_2.png
Έτσι μεέχουμε:
ενώ για τα βαρύκεντρα η κατάσταση είναι πιο απλή:
Eύκολα βλέπουμε ότικαι επομένως
και η ζητούμενη καθετότητα έπεται.
Κάποια σχόλια θα ακολουθήσουν...
 ,
,  που θα διαιρούσαν τις
που θα διαιρούσαν τις  ,
,  σε ίσους λόγους.
σε ίσους λόγους.  ,
,  είναι αρνητικά. Θα μπορούσαν λ.χ τα
είναι αρνητικά. Θα μπορούσαν λ.χ τα  ,
,  να είναι εσωτερικά των
να είναι εσωτερικά των  ,
, 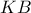 .
. ως
ως  (αυτοτεμνόμενο) κλπ.
(αυτοτεμνόμενο) κλπ.Δεν ξέρω που έκανα λάθος, έχω πάντως αντιπαράδειγμαnsmavrogiannis έγραψε: ↑Σάβ Μαρ 13, 2021 12:48 am"Όταν ζητείται να αποδείξουμε το συμπέρασμα με συνθετικές μεθόδους, χρησιμοποιούμε την εφευρετικότητα μας (ή αυτή ορισμένων άλλων ανθρώπων) αναζητώντας κατάλληλες μορφές και ιδέες στις οποίες μπορεί να βασιστεί η απόδειξη.
Όταν ζητείται να αποδείξουμε το συμπέρασμα με αναλυτικές μεθόδους, μπορούμε να προχωρήσουμε αμέσως για να εφαρμόσουμε μια
ισχυρή μέθοδος που αν κάνουμε την δουλειά σωστά δεν μπορεί να αποτύχει στην παραγωγή του αποτελέσματος."
 , τότε,
, τότε,  » έχουμε τις εξής γενικές (Γιάννη Ντάνη , Γεωμετρία) α) Την μέθοδο της Ανάλυσης, β) Την μέθοδο της Σύνθεσης, γ) Την μέθοδο της Άτοπο Απαγωγής, δ) Τη μέθοδο της Τέλειας Επαγωγής. Όταν μιλάμε για την Μέθοδο της Ανάλυσης εννοούμε την διαδικασία που κατέρχεται από αυτό που θέλουμε να αποδείξουμε «αν
» έχουμε τις εξής γενικές (Γιάννη Ντάνη , Γεωμετρία) α) Την μέθοδο της Ανάλυσης, β) Την μέθοδο της Σύνθεσης, γ) Την μέθοδο της Άτοπο Απαγωγής, δ) Τη μέθοδο της Τέλειας Επαγωγής. Όταν μιλάμε για την Μέθοδο της Ανάλυσης εννοούμε την διαδικασία που κατέρχεται από αυτό που θέλουμε να αποδείξουμε «αν  , τότε,
, τότε,  » δημιουργώντας ικανές συνθήκες, με το φραστικό «Αρκεί να Αποδείξουμε ότι, …. , Αρκεί να Αποδείξουμε ότι, …», έως ότου να καταλήξουμε σε Αληθή πρόταση (Προφανής ή με βάση τα θεωρητικά δεδομένα). Όμως πίσω από όλα αυτά υπάρχει μία διαδικασία του Νου που χωρίς αυτή δεν κάνουμε τίποτα. Είναι η διαδικασία Σκέψη– Ανάλυση πριν την επίλυση, που σίγουρα υπάρχει πριν τις μεθόδους που αναφέρουμε και είναι πιο εμφανής στην Αναλυτική μέθοδο Απόδειξης . Κατά την στιγμή της Ανάλυσης δύο είναι οι ας πούμε οι επιδιώξεις 1η ο λύτης να εισέρθει στον πυρήνα της κατασκευής του προβλήματος και να αποκαλύψει την «κρυμμένη» διαδρομή από την υπόθεση στο συμπέρασμα και 2η αν κάνει κάποια λάθος σκέψη, να την αντιληφθεί και να την χρησιμοποιήσει υπέρ του, ώστε να αλλάξει τμήμα ή ακόμα και όλη την σκέψη που τον οδήγησε στο λάθος, με στόχο να βρει τελικά το σωστό. Υπό αυτή την απόλυτα μοναδική Μαθηματική Αντίληψη ΔΕΝ υπάρχει «ουρανοκατέβατη» Συνθετική λύση (Και μιλάμε επί της Μαθηματικής ουσίας) και είναι καθαρό ότι, αν το ακούσουμε κάτι επιφανειακά τέτοιο, τότε, τρομάζει αφού πλανάται το ερώτημα: Πως σου ήρθε; Απλά σε πολλές περιπτώσεις η Ανάλυση δεν παρουσιάζεται και είναι φυσικό η άμεση και βίαια παρουσιασμένη Σύνθεση να Τρομάζει, όμως δεν γίνεται Σύνθεση αν ΔΕΝ έχει προηγηθεί η Ανάλυτική Διαδικασία Σκέψης (εκτός των περιπτώσεων εκείνων που κάποιος έχει μάθει απέξω την λύση και την παρουσιάζει). Καλώς λοιπόν παλαιότερα (διεθνώς) στα προβλήματα Πρακτικής Αριθμητικής ακολουθούνταν η διαδικασία παρουσίασης Σκέψη …… Λύση, και σίγουρα καλώς ο Γιάννης Ντάνης αναφέρει στο βιβλίο του: Με την μέθοδο της Σύνθεσης διατυπώνουμε μία πρόταση, ΑΦΟΥ ΠΡΩΤΑ ΜΕ ΤΗΝ ΑΝΑΛΥΣΗ (που δεν την διατυπώνουμε γραπτά) ανακαλύψουμε την Αληθή καταληκτική πρόταση
» δημιουργώντας ικανές συνθήκες, με το φραστικό «Αρκεί να Αποδείξουμε ότι, …. , Αρκεί να Αποδείξουμε ότι, …», έως ότου να καταλήξουμε σε Αληθή πρόταση (Προφανής ή με βάση τα θεωρητικά δεδομένα). Όμως πίσω από όλα αυτά υπάρχει μία διαδικασία του Νου που χωρίς αυτή δεν κάνουμε τίποτα. Είναι η διαδικασία Σκέψη– Ανάλυση πριν την επίλυση, που σίγουρα υπάρχει πριν τις μεθόδους που αναφέρουμε και είναι πιο εμφανής στην Αναλυτική μέθοδο Απόδειξης . Κατά την στιγμή της Ανάλυσης δύο είναι οι ας πούμε οι επιδιώξεις 1η ο λύτης να εισέρθει στον πυρήνα της κατασκευής του προβλήματος και να αποκαλύψει την «κρυμμένη» διαδρομή από την υπόθεση στο συμπέρασμα και 2η αν κάνει κάποια λάθος σκέψη, να την αντιληφθεί και να την χρησιμοποιήσει υπέρ του, ώστε να αλλάξει τμήμα ή ακόμα και όλη την σκέψη που τον οδήγησε στο λάθος, με στόχο να βρει τελικά το σωστό. Υπό αυτή την απόλυτα μοναδική Μαθηματική Αντίληψη ΔΕΝ υπάρχει «ουρανοκατέβατη» Συνθετική λύση (Και μιλάμε επί της Μαθηματικής ουσίας) και είναι καθαρό ότι, αν το ακούσουμε κάτι επιφανειακά τέτοιο, τότε, τρομάζει αφού πλανάται το ερώτημα: Πως σου ήρθε; Απλά σε πολλές περιπτώσεις η Ανάλυση δεν παρουσιάζεται και είναι φυσικό η άμεση και βίαια παρουσιασμένη Σύνθεση να Τρομάζει, όμως δεν γίνεται Σύνθεση αν ΔΕΝ έχει προηγηθεί η Ανάλυτική Διαδικασία Σκέψης (εκτός των περιπτώσεων εκείνων που κάποιος έχει μάθει απέξω την λύση και την παρουσιάζει). Καλώς λοιπόν παλαιότερα (διεθνώς) στα προβλήματα Πρακτικής Αριθμητικής ακολουθούνταν η διαδικασία παρουσίασης Σκέψη …… Λύση, και σίγουρα καλώς ο Γιάννης Ντάνης αναφέρει στο βιβλίο του: Με την μέθοδο της Σύνθεσης διατυπώνουμε μία πρόταση, ΑΦΟΥ ΠΡΩΤΑ ΜΕ ΤΗΝ ΑΝΑΛΥΣΗ (που δεν την διατυπώνουμε γραπτά) ανακαλύψουμε την Αληθή καταληκτική πρόταση  και τον δρόμο (επιστροφής) από αυτή μέχρι το συμπέρασμα
και τον δρόμο (επιστροφής) από αυτή μέχρι το συμπέρασμα 
 Η βασική λειτουργία του κέντρου βάρους είναι ο λόγος
Η βασική λειτουργία του κέντρου βάρους είναι ο λόγος  Αυτό μας οδηγεί στο σημείο της σκέψης: Θέλουμε
Αυτό μας οδηγεί στο σημείο της σκέψης: Θέλουμε  που λόγω του Θεωρήματος του Θαλή ΑΡΚΕΙ ΝΑ ΑΠΟΔΕΊΞΟΥΜΕ
που λόγω του Θεωρήματος του Θαλή ΑΡΚΕΙ ΝΑ ΑΠΟΔΕΊΞΟΥΜΕ  Όμως θα πρέπει να συνδέσουμε τα ΟΡΘΟΚΕΝΤΡΑ σε άλλα τρίγωνα, με το ευθύγραμμο τμήμα
Όμως θα πρέπει να συνδέσουμε τα ΟΡΘΟΚΕΝΤΡΑ σε άλλα τρίγωνα, με το ευθύγραμμο τμήμα  Αν σκεφτούμε λίγο υπάρχει κάτι κοινό η καθετότητα
Αν σκεφτούμε λίγο υπάρχει κάτι κοινό η καθετότητα  που για να συνδεθεί με την θέση
που για να συνδεθεί με την θέση  αυτό επιτυγχάνεται μέσω της καθετότητας
αυτό επιτυγχάνεται μέσω της καθετότητας  ,
,  μέσο της
μέσο της  (Από το σχήμα στην λύση μου) και αντίστοιχα από την απέναντι πλευρά οπότε «στύβουμε» το κεφάλι μας να πάμε στην ομοιότητα των τριγώνων
(Από το σχήμα στην λύση μου) και αντίστοιχα από την απέναντι πλευρά οπότε «στύβουμε» το κεφάλι μας να πάμε στην ομοιότητα των τριγώνων και εκεί μας εξυπηρετεί το λήμμα που η δημιουργία του έρχεται αν βέβαια γνωρίζουμε το αντίστοιχο θεωρητικό δεδομένο του θεωρήματος του Euler (τοποθέτηση δηλαδή της στιγμής εκείνης του προβλήματος στην κατάλληλη θεωρητική γνώση). Τελικά όπως και να λυθεί ένα θέμα είναι αποδεκτό και σίγουρα δεν γίνεται να υπάρχει Συνθετική Λύση με την έννοια του «ουρανοκατέβατου», αφού προηγείται η διαδικασία ΑΝΑΛΥΣΗ. Υπάρχει δε και το ενδεχόμενο να επιλύεται με «πάντρεμα» δύο Μαθηματικών θεωρήσεων π.χ. να συνυπάρχουν στην λύση του προβλήματος σταλίδες (Τίτλος από το βιβλίο Γεωμετρίας του κ. Μπαλόγλου) Ευκλείδειας Γεωμετρίας και σταλίδες Διανυσματικής Γεωμετρίας ίσως και σταλίδες Ανάλυσης κτλ.
και εκεί μας εξυπηρετεί το λήμμα που η δημιουργία του έρχεται αν βέβαια γνωρίζουμε το αντίστοιχο θεωρητικό δεδομένο του θεωρήματος του Euler (τοποθέτηση δηλαδή της στιγμής εκείνης του προβλήματος στην κατάλληλη θεωρητική γνώση). Τελικά όπως και να λυθεί ένα θέμα είναι αποδεκτό και σίγουρα δεν γίνεται να υπάρχει Συνθετική Λύση με την έννοια του «ουρανοκατέβατου», αφού προηγείται η διαδικασία ΑΝΑΛΥΣΗ. Υπάρχει δε και το ενδεχόμενο να επιλύεται με «πάντρεμα» δύο Μαθηματικών θεωρήσεων π.χ. να συνυπάρχουν στην λύση του προβλήματος σταλίδες (Τίτλος από το βιβλίο Γεωμετρίας του κ. Μπαλόγλου) Ευκλείδειας Γεωμετρίας και σταλίδες Διανυσματικής Γεωμετρίας ίσως και σταλίδες Ανάλυσης κτλ.



 , εσωτερικό του σημείο
, εσωτερικό του σημείο  τέτοιο ώστε
τέτοιο ώστε  και σημεία
και σημεία  Αν
Αν  είναι τα ορθόκεντρα των τριγώνων
είναι τα ορθόκεντρα των τριγώνων  αντίστοιχα να αποδείξετε ότι
αντίστοιχα να αποδείξετε ότι 
Ευχαριστούμε πολύ. Δύσκολο αλλά ενδιαφέρον άρθρο.min## έγραψε: ↑Σάβ Μαρ 13, 2021 2:40 amΚαλησπέρα κι από μένα.
Απλώς να αναφέρω ότι πρόκειται ουσιαστικά για αναδιατύπωση της κλασικής* ιδιότητας :"Η ευθεία Newton-Gauss ενός πλήρους τετραπλεύρου είναι κάθετη στην ευθεία Steiner-Aubert του".
Αρκεί κανείς να δει τοως
(αυτοτεμνόμενο) κλπ.
*Βλ.Ιδιότητα 7 εδώ https://forumgeom.fau.edu/FG2004volume4/FG200405.pdf
Γιώργο δεν θα ονόμαζα την άσκηση αντιπαράδειγμα. Θα προτιμούσα τον χαρακτηρισμό ακραίο παράδειγμα. Η αιτιολόγηση της επιλογής νομίζω θα φανεί στα επόμενα.gbaloglou έγραψε: ↑Σάβ Μαρ 13, 2021 7:34 pmΔεν ξέρω που έκανα λάθος, έχω πάντως αντιπαράδειγμαnsmavrogiannis έγραψε: ↑Σάβ Μαρ 13, 2021 12:48 am"Όταν ζητείται να αποδείξουμε το συμπέρασμα με συνθετικές μεθόδους, χρησιμοποιούμε την εφευρετικότητα μας (ή αυτή ορισμένων άλλων ανθρώπων) αναζητώντας κατάλληλες μορφές και ιδέες στις οποίες μπορεί να βασιστεί η απόδειξη.
Όταν ζητείται να αποδείξουμε το συμπέρασμα με αναλυτικές μεθόδους, μπορούμε να προχωρήσουμε αμέσως για να εφαρμόσουμε μια
ισχυρή μέθοδος που αν κάνουμε την δουλειά σωστά δεν μπορεί να αποτύχει στην παραγωγή του αποτελέσματος."
 ,
,  με κέντρα
με κέντρα  ,
,  εφάπτονται εξωτερικά στο
εφάπτονται εξωτερικά στο  και μία κοινή εξωτερική εφαπτομένη τους
και μία κοινή εξωτερική εφαπτομένη τους  εφάπτεται σε αυτούς στα
εφάπτεται σε αυτούς στα  ,
,  . Από το
. Από το  φέρνουμε εφαπτομένη στον
φέρνουμε εφαπτομένη στον  ώστε το σημείο επαφής και τα
ώστε το σημείο επαφής και τα  ,
,  να βρίσκονται εκατέρωθεν της διακέντρου η οποία τέμνει την κοινή εσωτερική εφαπτομένη
να βρίσκονται εκατέρωθεν της διακέντρου η οποία τέμνει την κοινή εσωτερική εφαπτομένη  στο
στο  . Από το
. Από το  φέρνουμε εφαπτόμενη
φέρνουμε εφαπτόμενη  στον
στον  διάφορη της
διάφορη της  . H
. H  τέμνει τον
τέμνει τον  σε δύο σημεία. Έστω
σε δύο σημεία. Έστω  εκείνο το τέτοιο ώστε το άλλο σημείο τομής να βρίσκεται μεταξύ των
εκείνο το τέτοιο ώστε το άλλο σημείο τομής να βρίσκεται μεταξύ των 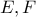 . Να αποδειχθεί ότι η
. Να αποδειχθεί ότι η  είναι παράλληλη στην
είναι παράλληλη στην  .
. έχει ακτίνα μικρότερη ή ίση του
έχει ακτίνα μικρότερη ή ίση του  και ότι ο
και ότι ο  έχει ακτίνα
έχει ακτίνα  και έτσι λόγω ομοιότητας καλύπτονται όλες οι περιπτώσεις.
και έτσι λόγω ομοιότητας καλύπτονται όλες οι περιπτώσεις.  είναι ο μοναδιαίος κύκλος
είναι ο μοναδιαίος κύκλος  και ότι ο
και ότι ο  , ότι η κοινή εσωτερική εφαπτομένη είναι η
, ότι η κοινή εσωτερική εφαπτομένη είναι η  και για να παραμετροποιήσουμε το πρόβλημα ότι ο
και για να παραμετροποιήσουμε το πρόβλημα ότι ο  είναι στοιχείο της δέσμης που ορίζουν ο
είναι στοιχείο της δέσμης που ορίζουν ο  με την
με την  δηλαδή ότι είναι ο κύκλος
δηλαδή ότι είναι ο κύκλος με
με  .
. είναι μικρότερη του
είναι μικρότερη του  δηλαδή
δηλαδή  . Στην περίπτωση αυτή οι δύο κύκλοι είναι ομοιόθετοι με μία εξωτερική ομοιοθεσία από της οποίας το κέντρο διέρχεται και η
. Στην περίπτωση αυτή οι δύο κύκλοι είναι ομοιόθετοι με μία εξωτερική ομοιοθεσία από της οποίας το κέντρο διέρχεται και η  . Ας το ονομάσουμε
. Ας το ονομάσουμε  . Δεδομένου ότι τα κέντρα των
. Δεδομένου ότι τα κέντρα των  ,
,  είναι τα
είναι τα  και
και  και οι ακτίνες είναι
και οι ακτίνες είναι  και
και 
 και επομένως
και επομένως  και το κέντρο ομοιόθεσίας είναι το
και το κέντρο ομοιόθεσίας είναι το  .
. θα βρούμε την κοινή εξωτερική εφαπτομένη
θα βρούμε την κοινή εξωτερική εφαπτομένη  ως εκείνη την εφαπτομένη
ως εκείνη την εφαπτομένη  του
του  που διέρχεται από το
που διέρχεται από το  . Βρίσκουμε διαδοχικά ότι
. Βρίσκουμε διαδοχικά ότι  και επομένως
και επομένως  .
.  στον
στον  υπολογίζεται παρόμοια και είναι η
υπολογίζεται παρόμοια και είναι η  η οποία τέμνει την
η οποία τέμνει την  στο
στο  .
.  αρκεί να βρούμε ευθεία με συντελεστή διευθύνσεως
αρκεί να βρούμε ευθεία με συντελεστή διευθύνσεως  που διέρχεται από το
που διέρχεται από το  και απέχει από το κέντρο του
και απέχει από το κέντρο του  απόσταση όση η ακτίνα του. Δηλαδή αναζητούμε ευθεία της μορφής
απόσταση όση η ακτίνα του. Δηλαδή αναζητούμε ευθεία της μορφής  που απέχει από το
που απέχει από το  απόσταση
απόσταση  . Καταλήγουμε στην σχέση
. Καταλήγουμε στην σχέση 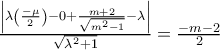
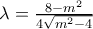 .
. έχει εξίσωση:
έχει εξίσωση:
 λύνοντας το δευτεροβάθμιο σύστημα των εξισώσεων της παραπάνω ευθείας και του
λύνοντας το δευτεροβάθμιο σύστημα των εξισώσεων της παραπάνω ευθείας και του  μπορούμε να γλυτώσουμε κάποιες πράξεις εργαζόμενοι διαφορετικά: Βρίσκουμε την από το
μπορούμε να γλυτώσουμε κάποιες πράξεις εργαζόμενοι διαφορετικά: Βρίσκουμε την από το  παράλληλη στην
παράλληλη στην  και απαιτούμε το σημείο τομής της με την
και απαιτούμε το σημείο τομής της με την  να ανήκει στον
να ανήκει στον  . Η ευθεία αυτή εύκολα βρίσκεται και είναι η
. Η ευθεία αυτή εύκολα βρίσκεται και είναι η 
 των
των  ,
,  να ανήκει στον
να ανήκει στον  . Αν ονομάσουμε
. Αν ονομάσουμε  ις ορίζουσες του συστήματος
ις ορίζουσες του συστήματος  θέλουμε
θέλουμε 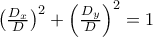 η ισοδύναμα
η ισοδύναμα .
.




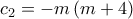
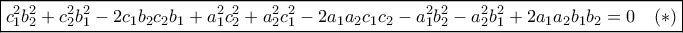



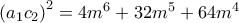
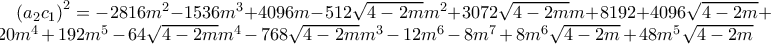




 επαληθεύεται για αυτές τις τιμές.
επαληθεύεται για αυτές τις τιμές.  και
και  έχουν ίσες ακτίνες δηλαδή όταν
έχουν ίσες ακτίνες δηλαδή όταν  . H περίπτωση αυτή καλύπτεται από εκείνη όπου
. H περίπτωση αυτή καλύπτεται από εκείνη όπου  παίρνοντας όρια για
παίρνοντας όρια για  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες