R^3 ΚΑΙ ΠΑΛΙ
Συντονιστές: vittasko, silouan, Doloros
- S.E.Louridas
- Δημοσιεύσεις: 5956
- Εγγραφή: Σάβ Μαρ 21, 2009 10:53 am
- Τοποθεσία: Aegaleo.
- Επικοινωνία:
R^3 ΚΑΙ ΠΑΛΙ
Να τμηθεί πρισματική επιφάνεια κατά τρίγωνο όμοιο προς δοθέν.
S.E.Louridas
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
Λέξεις Κλειδιά:
Re: R^3 ΚΑΙ ΠΑΛΙ
S.E.Louridas έγραψε: ↑Τετ Φεβ 24, 2021 10:51 pmΝα τμηθεί πρισματική επιφάνεια κατά τρίγωνο όμοιο προς δοθέν.
Σωτήρη καλησπέρα....
Εργαζόμαστε στο ακόλουθο σχήμα:
Στο σχήμα αυτό βλέπουμε ένα ορθό τριγωνικό πρίσμα
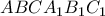 ,
,το οποίο προήλθε από την δοθείσα πρισματική επιφάνεια(τριγωνική ή και
πολυγωνική γενικότερα).
Ακόμα βλέπουμε το δοθέν τρίγωνο
 .
. Έστω τώρα ότι το τρίγωνο
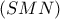 όπου
όπου 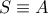 είναι το ζητούμενο.
είναι το ζητούμενο.Δηλαδή
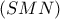 όμοιο με το
όμοιο με το  . Δηλαδή:
. Δηλαδή: 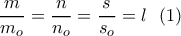
όπου
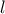 ο λόγος ομοιότητας αυτών.
ο λόγος ομοιότητας αυτών.Από τα ορθογώνια τρίγωνα
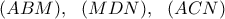 προκύπτει:
προκύπτει: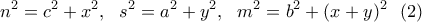
Από τις εξισώσεις (2) ακόμα προκύπτει:
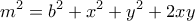
και από την (1) θα είναι:
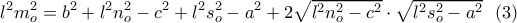
Η εξίσωση αυτή έχει άγνωστο το λόγο ομοιότητας
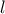 και τελικά μετά πράξεις καταλήγει στη μορφή:
και τελικά μετά πράξεις καταλήγει στη μορφή:
όπου:
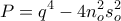

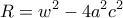
και
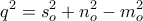
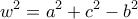 .
. Τελικά η λύσεις της (4) δίνει και εκείνες που θα δώσουν τις τιμές των πλευρών
του ζητούμενου τριγώνου.
Το σχήμα που ανάρτησα έχει κατασκευαστεί αφού λύθηκε η εξίσωση (4).
Κώστας Δόρτσιος
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες
