Σωτήρη χαιρετίζω την συνεχιζόμενη σταυροφορία σου υπέρ του "δικού μας χώρου" και καταθέτω κάποιες σκέψεις (μάλλον ημιτελείς) για την σοφά επιλεγμένη τριλογία σου:
Στο πρώτο πρόβλημα έχουμε απειρία λύσεων, και αυτό προκύπτει από τα δύο επόμενα προβλήματα ως εξής: θεωρούμε αυθαίρετο τρίτο σημείο

και κατασκευάζουμε την μοναδική σφαίρα (δεύτερο πρόβλημα) ή μία από τις δύο σφαίρες (τρίτο πρόβλημα) που διέρχεται από τα σημεία

,

,

και εφάπτεται του επιπέδου

-- (σχεδόν) για κάθε

προκύπτει και διαφορετική σφαίρα. [Μπορούμε να χρησιμοποιήσουμε είτε το δεύτερο πρόβλημα είτε το τρίτο πρόβλημα αν

, αλλιώς πάμε υποχρεωτικά στο τρίτο πρόβλημα.]
Στο δεύτερο πρόβλημα τα πράγματα είναι απλά: γνωρίζουμε εκ των προτέρων το σημείο επαφής

της ζητούμενης σφαίρας με το επίπεδο

, καθώς αυτό είναι υποχρεωτικά το σημείο τομής του

με την 'περίκεντρη ευθεία' του

, την ευθεία
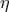
δηλαδή που είναι κάθετη στο επίπεδο του

και διέρχεται δια του περικέντρου του^ για να βρούμε το κέντρο

της ζητούμενης σφαίρας, αρκεί να βρούμε την τομή της
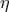
με τον γεωμετρικό τόπο των σημείων που ισαπέχουν από το

και από ένα εκ των

,

,

, που είναι βέβαια το αντίστοιχο μεσοκάθετο επίπεδο. (Οι τομές των τριών μεσοκαθέτων επιπέδων με την περίκεντρη ευθεία ταυτίζονται, και η τομή αυτή είναι βεβαίως το κέντρο

της σφαίρας, ενώ ακτίνα της είναι η

.)
Στο τρίτο πρόβλημα ο βαθμός δυσκολίας ανεβαίνει, καθώς ο κρίσιμος γεωμετρικός τόπος δεν είναι πλέον το σύνολο των σημείων που ισαπέχουν από δύο σημεία, αλλά το σύνολο των σημείων που ισαπέχουν από σημείο και επίπεδο: ήδη γνωρίζουμε ότι το

κείται επί της
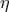
, θέλουμε τώρα να ισαπέχει από το

και από τα

,

,

, οπότε το

προκύπτει ως τομή της
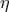
και τριών παραβολοειδών, ουσιαστικά ως τομή της
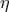
και ενός παραβολοειδούς. [Σε αντίθεση με το δεύτερο πρόβλημα (μοναδική λύση) εδώ έχουμε δύο λύσεις (όσα και τα σημεία τομής ευθείας και παραβολοειδούς).]
Είναι όμως αυτό το καλύτερο που μπορούμε να κάνουμε, και που μας οδηγεί η εμπειρία του διδιάστατου χώρου; Αν είχαμε να βρούμε τον κύκλο που διέρχεται από δύο σημεία

,

και εφάπτεται ευθείας

... θα βρίσκαμε το κέντρο του ως τομή της μεσοκαθέτου της

και δύο (ουσιαστικά μιας) παραβολών; Ισχύει βεβαίως και αυτό, υπάρχουν όμως και άλλες κατασκευές, όπως αυτή
εδώ (πιθανώς κλασσική). Μπορούμε να κάνουμε κάτι ανάλογο στον τριδιάστατο χώρο; Ας το σκεφτούμε!
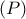 και δύο σημεία
και δύο σημεία  που δεν ανήκουν σε αυτό και ανήκουν στον ίδιο ημιχώρο από τους δύο που το επίπεδο
που δεν ανήκουν σε αυτό και ανήκουν στον ίδιο ημιχώρο από τους δύο που το επίπεδο 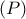 χωρίζει τον χώρο. Να κατασκευαστεί σφαίρα που διέρχεται από τα σημεία
χωρίζει τον χώρο. Να κατασκευαστεί σφαίρα που διέρχεται από τα σημεία  και εφάπτεται στο επίπεδο
και εφάπτεται στο επίπεδο  Πόσες τέτοιες σφαίρες υπάρχουν;
Πόσες τέτοιες σφαίρες υπάρχουν; 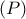 και τρία σημεία
και τρία σημεία  που δεν ανήκουν στην ίδια ευθεία, δεν ανήκουν στο επίπεδο
που δεν ανήκουν στην ίδια ευθεία, δεν ανήκουν στο επίπεδο 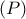 , αλλά ανήκουν σε επίπεδο παράλληλο στο
, αλλά ανήκουν σε επίπεδο παράλληλο στο  Να κατασκευαστεί σφαίρα που διέρχεται από τα σημεία
Να κατασκευαστεί σφαίρα που διέρχεται από τα σημεία  και εφάπτεται στο επίπεδο
και εφάπτεται στο επίπεδο  Πόσες τέτοιες σφαίρες υπάρχουν;
Πόσες τέτοιες σφαίρες υπάρχουν;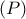 και τρία σημεία
και τρία σημεία  που δεν ανήκουν στην ίδια ευθεία, δεν ανήκουν στο επίπεδο
που δεν ανήκουν στην ίδια ευθεία, δεν ανήκουν στο επίπεδο 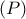 , ανήκουν σε επίπεδο μη παράλληλο στο
, ανήκουν σε επίπεδο μη παράλληλο στο 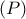 και ανήκουν στον ίδιο ημιχώρο από τους δύο που το επίπεδο
και ανήκουν στον ίδιο ημιχώρο από τους δύο που το επίπεδο 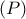 χωρίζει τον χώρο. Να κατασκευαστεί σφαίρα που διέρχεται από τα σημεία
χωρίζει τον χώρο. Να κατασκευαστεί σφαίρα που διέρχεται από τα σημεία  και εφάπτεται στο επίπεδο
και εφάπτεται στο επίπεδο  Πόσες τέτοιες σφαίρες υπάρχουν;
Πόσες τέτοιες σφαίρες υπάρχουν;
 και κατασκευάζουμε την μοναδική σφαίρα (δεύτερο πρόβλημα) ή μία από τις δύο σφαίρες (τρίτο πρόβλημα) που διέρχεται από τα σημεία
και κατασκευάζουμε την μοναδική σφαίρα (δεύτερο πρόβλημα) ή μία από τις δύο σφαίρες (τρίτο πρόβλημα) που διέρχεται από τα σημεία  ,
,  ,
,  -- (σχεδόν) για κάθε
-- (σχεδόν) για κάθε  , αλλιώς πάμε υποχρεωτικά στο τρίτο πρόβλημα.]
, αλλιώς πάμε υποχρεωτικά στο τρίτο πρόβλημα.] της ζητούμενης σφαίρας με το επίπεδο
της ζητούμενης σφαίρας με το επίπεδο  , την ευθεία
, την ευθεία 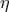 δηλαδή που είναι κάθετη στο επίπεδο του
δηλαδή που είναι κάθετη στο επίπεδο του  της ζητούμενης σφαίρας, αρκεί να βρούμε την τομή της
της ζητούμενης σφαίρας, αρκεί να βρούμε την τομή της  .)
.) ... θα βρίσκαμε το κέντρο του ως τομή της μεσοκαθέτου της
... θα βρίσκαμε το κέντρο του ως τομή της μεσοκαθέτου της  και δύο (ουσιαστικά μιας) παραβολών; Ισχύει βεβαίως και αυτό, υπάρχουν όμως και άλλες κατασκευές, όπως αυτή
και δύο (ουσιαστικά μιας) παραβολών; Ισχύει βεβαίως και αυτό, υπάρχουν όμως και άλλες κατασκευές, όπως αυτή  να πηγάζει από το πάλαι ποτέ ρηθέν: «Αν δεν κοιτάξεις το σπίτι σου, τότε, θα πέσει και θα σε πλακώσει» (Ψυχολογία βάθους γαρ).
να πηγάζει από το πάλαι ποτέ ρηθέν: «Αν δεν κοιτάξεις το σπίτι σου, τότε, θα πέσει και θα σε πλακώσει» (Ψυχολογία βάθους γαρ). της σφαίρας με το επίπεδο
της σφαίρας με το επίπεδο 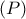 και θεωρήσουμε
και θεωρήσουμε  τότε, ο περιγεγραμμένος κύκλος στο τρίγωνο
τότε, ο περιγεγραμμένος κύκλος στο τρίγωνο  εφάπτεται στην ευθεία
εφάπτεται στην ευθεία 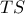 και ο περιγεγραμμένος κύκλος στο τρίγωνο
και ο περιγεγραμμένος κύκλος στο τρίγωνο 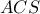 θα εφάπτεται στην ευθεία
θα εφάπτεται στην ευθεία  Άρα παίρνουμε:
Άρα παίρνουμε:  και
και 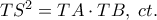 Επομένως προσδιορίζεται στο επίπεδο
Επομένως προσδιορίζεται στο επίπεδο  και
και 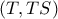 (Είναι μάλιστα εν γένει δύο τα σημεία τομής , ως τομές δύο κύκλων, άρα τελικά εν γένει θα έχουμε αντίστοιχα δύο σφαίρες). Έτσι με βάση τα σταθερά τρίγωνα
(Είναι μάλιστα εν γένει δύο τα σημεία τομής , ως τομές δύο κύκλων, άρα τελικά εν γένει θα έχουμε αντίστοιχα δύο σφαίρες). Έτσι με βάση τα σταθερά τρίγωνα  κατασκευάζουμε την ζητούμενη σφαίρα με κέντρο την τομή των αντίστοιχων κάθετων ευθειών στα επίπεδα των τριγώνων
κατασκευάζουμε την ζητούμενη σφαίρα με κέντρο την τομή των αντίστοιχων κάθετων ευθειών στα επίπεδα των τριγώνων  , το οποίο είναι το σημείο επαφής της σφαίρας
, το οποίο είναι το σημείο επαφής της σφαίρας  , κινείται πάνω στον κύκλο:
, κινείται πάνω στον κύκλο: 
 με
με  , η οποία τέμνει το επίπεδο
, η οποία τέμνει το επίπεδο  . Προβάλουμε επίσης το
. Προβάλουμε επίσης το  η προβολή. Βεβαίως το κέντρο
η προβολή. Βεβαίως το κέντρο 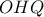 , και η προβολή
, και η προβολή  είναι το ζητούμενο σημείο επαφής. Στο επίπεδο
είναι το ζητούμενο σημείο επαφής. Στο επίπεδο  και
και  , από τα οποία λαμβάνουμε
, από τα οποία λαμβάνουμε
 ,
, 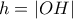 ,
,  η ακτίνα του περίκυκλου του
η ακτίνα του περίκυκλου του  η ακτίνα της ζητούμενης σφαίρας (οπότε
η ακτίνα της ζητούμενης σφαίρας (οπότε  ).
). , λαμβάνουμε
, λαμβάνουμε
 .
.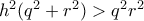 , βεβαίως μία από αυτές ενδέχεται να είναι μη θετική, οπότε και απορρίπτεται. (Απόλυτα συμβατά αυτά με την προηγούμενη προσέγγιση μου (#2), όπου το κέντρο
, βεβαίως μία από αυτές ενδέχεται να είναι μη θετική, οπότε και απορρίπτεται. (Απόλυτα συμβατά αυτά με την προηγούμενη προσέγγιση μου (#2), όπου το κέντρο  ... δεν υπάρχει περίπτωση αρνητικού
... δεν υπάρχει περίπτωση αρνητικού  . Άρα, ή δεν υπάρχει λύση ή υπάρχουν δύο λύσεις, με μόνη εξαίρεση την περίπτωση
. Άρα, ή δεν υπάρχει λύση ή υπάρχουν δύο λύσεις, με μόνη εξαίρεση την περίπτωση  .
.  τότε προφανώς η
τότε προφανώς η 
 . (με πράσινο χρώμα)
. (με πράσινο χρώμα) της ζητούμενης σφαίρας θα είναι επί της καθέτου στο επίπεδο του τριγώνου αυτού και μάλιστα
της ζητούμενης σφαίρας θα είναι επί της καθέτου στο επίπεδο του τριγώνου αυτού και μάλιστα . Άρα το σημείο
. Άρα το σημείο  και
και  , στηριζόμενοι στο επίπεδο που ορίζεται από τα τμήματα
, στηριζόμενοι στο επίπεδο που ορίζεται από τα τμήματα 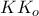 , όπου
, όπου  είναι το περίκεντρο του τριγώνου
είναι το περίκεντρο του τριγώνου  ,
,  το οποίο
το οποίο  και ακτίνας
και ακτίνας  με την εφαπτόμενη ευθεία, όπου
με την εφαπτόμενη ευθεία, όπου  κατασκευάστηκαν επί του επιπέδου
κατασκευάστηκαν επί του επιπέδου  και
και  και επί των αντιστοίχων επιπέδων προφανώς τέμνονται στο κέντρο της ζητούμενης σφαίρας.
και επί των αντιστοίχων επιπέδων προφανώς τέμνονται στο κέντρο της ζητούμενης σφαίρας. τότε έχουμε το ακόλουθο σχήμα:
τότε έχουμε το ακόλουθο σχήμα:  κλπ), με τον περίκυκλο του
κλπ), με τον περίκυκλο του  ): στην περίπτωση αυτή και μόνον οι δύο κύκλοι του Σωτήρη -- που μας έδειξε υπέροχα ο Κώστας -- εφάπτονται αλλήλων και η αναζητούμενη σφαίρα είναι μοναδική, με ακτίνα
): στην περίπτωση αυτή και μόνον οι δύο κύκλοι του Σωτήρη -- που μας έδειξε υπέροχα ο Κώστας -- εφάπτονται αλλήλων και η αναζητούμενη σφαίρα είναι μοναδική, με ακτίνα  , κέντρο επί της
, κέντρο επί της  από το περίκεντρο του
από το περίκεντρο του  , και αυτό φαίνεται από τα δύο σχήματα στην δεξιά πλευρά του συνημμένου: στην πάνω περίπτωση (κόκκινο
, και αυτό φαίνεται από τα δύο σχήματα στην δεξιά πλευρά του συνημμένου: στην πάνω περίπτωση (κόκκινο  που ο περίκυκλος του
που ο περίκυκλος του  (Πρόβλημα 2 του Σωτήρη) --
(Πρόβλημα 2 του Σωτήρη) -- 
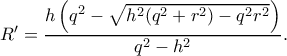
 , ισοδύναμη προς την προφανώς ισχύουσα
, ισοδύναμη προς την προφανώς ισχύουσα  .
.  , ισοδύναμη (ύστερα από πράξεις και ύψωση στο τετράγωνο) προς την
, ισοδύναμη (ύστερα από πράξεις και ύψωση στο τετράγωνο) προς την 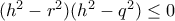 , και, λόγω και της δοθείσης
, και, λόγω και της δοθείσης 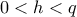 , προς την
, προς την 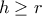 .
.
 του περίκεντρου
του περίκεντρου  όπου
όπου  το περίκεντρο του τριγώνου
το περίκεντρο του τριγώνου  ,
,  η απόσταση του σημείου
η απόσταση του σημείου  .
.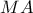 θεωρήσουμε την απόσταση
θεωρήσουμε την απόσταση  , όπου
, όπου  είναι ένα από τα σημεία τομής
είναι ένα από τα σημεία τομής 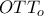 , τότε το ζητούμενο σημείο είναι
, τότε το ζητούμενο σημείο είναι 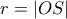 και
και 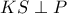 . Η πιο ενδιαφέρουσα περίπτωση, που ήδη είχα παρουσιάσει προ ημερών, είναι αυτή του κόκκινου
. Η πιο ενδιαφέρουσα περίπτωση, που ήδη είχα παρουσιάσει προ ημερών, είναι αυτή του κόκκινου 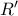 της εσωτερικής σφαίρας ισχύει πάντοτε η
της εσωτερικής σφαίρας ισχύει πάντοτε η  , οπότε η εσωτερική σφαίρα δεν υπάρχει όταν
, οπότε η εσωτερική σφαίρα δεν υπάρχει όταν 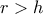 και γίνεται εξωτερική!
και γίνεται εξωτερική! ,
,  ,
,  ,
,  ,
,  :
:

 ,
, 
 ,
, 
 ,
, 
 και η απόσταση του κέντρου της από το
και η απόσταση του κέντρου της από το  , ενώ η ακτίνα της μικρής σφαίρας τείνει προς το
, ενώ η ακτίνα της μικρής σφαίρας τείνει προς το  και η απόσταση του κέντρου της από το
και η απόσταση του κέντρου της από το  . Επίσης για
. Επίσης για  οι ακτίνες μεγάλης και μικρής σφαίρας έχουν μήκη
οι ακτίνες μεγάλης και μικρής σφαίρας έχουν μήκη  και
και  , και οι αποστάσεις των αντίστοιχων κέντρων από το
, και οι αποστάσεις των αντίστοιχων κέντρων από το  και
και 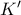 κείνται στην ίδια πλευρά του
κείνται στην ίδια πλευρά του  , οπότε
, οπότε  και
και  , ενώ
, ενώ 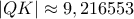 και
και  . Τέλος, για
. Τέλος, για  έχουμε την αναμενόμενη ισότητα ακτίνων (
έχουμε την αναμενόμενη ισότητα ακτίνων (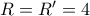 ) και ταύτιση κέντρων (
) και ταύτιση κέντρων ( ).
). για
για  για
για  για
για  (και ο κόκκινος δίσκος στην αρχή των αξόνων
(και ο κόκκινος δίσκος στην αρχή των αξόνων  είναι εκείνη που έχει εστία το σημείο
είναι εκείνη που έχει εστία το σημείο  και διευθετούσα την ευθεία
και διευθετούσα την ευθεία  .
. 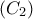 έχει εστία το σημείο
έχει εστία το σημείο  και διευθετούσα την ευθεία
και διευθετούσα την ευθεία 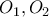 του ζητούμενου κύκλου.
του ζητούμενου κύκλου.