Καλησπέρα.
Εξαιρετικό πρόβλημα-αν και ψιλοαδύνατο να λυθεί (συνθετικά) χωρίς τη βοήθεια λογισμικού.
Η παρακάτω λύση είναι μεν μακροσκελής,αλλά συνδυάζει πολλά πράγματα οπότε:
Λήμμα 01. (χωρίς σχήμα)
Έστω τρίγωνο

,
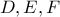
τα μέσα των τόξων

και

τυχαίο σημείο στο μικρό τόξο

.
Αν

,τότε το κέντρο του

βρίσκεται στην

.
Απόδειξη:
Απλή.Ας είναι

τα συμμετρικά των

προς την

.Για να μην παίζουμε με προσανατολισμένες γωνίες,θεωρούμε πως η

βρίσκεται πιο κοντά στο

από την

.
Από κυνήγι γωνιών βρίσκουμε πως

οπότε

εγγράψιμο.
Όμως

εγγράψιμο ως τραπέζιο,οπότε

ομοκυκλικά και συνεπώς ο

έχει άξονα συμμετρίας την

.

Σημ.Μπορούμε να δούμε αυτό το Λήμμα ως γενίκευση γνωστής ιδιότητας του μικτεγγεγραμμένου.
Λήμμα 1.(σχήμα 1)
Έστω τρίγωνο

,

το κέντρο του

,

τα έκκέντρα των

και

το μέσο του τόξου

.
Τότε

εγγράψιμο.

- Lemma 1..png (19.14 KiB) Προβλήθηκε 1429 φορές
Απόδειξη:
Θεωρούμε την ομοιοθεσία κέντρου

και λόγου

,η οποία στέλνει το

στο αντιδιαμετρικό του

-έστω

-στον

.
Τα

πάνε προφανώς στις τομές των

τις οποίες και ονομάζουμε

αντίστοιχα.
Από το
Λήμμα 01. για το τρίγωνο

προκύπτει πως το κέντρο

του

βρίσκεται στην

.
Άρα το συμμετρικό του

ως προς την

(ας πούμε

) βρίσκεται στον

.
Επειδή

,το

είναι το μέσον του

οπότε εφαρμόζοντας την αντίστροφη ομοιοθεσία (λόγου

) παίρνουμε πως το

ανήκει στον

.

Πίσω στο πρόβλημα τώρα:

- κυρίως.png (33.47 KiB) Προβλήθηκε 1429 φορές
Ας είναι

τα μέσα των

αντίστοιχα και

τα έκκεντρα των

(αντίστοιχα).
Προφανώς οι

είναι συνευθειακές τριάδες.
Ορίζουμε τώρα

και κυκλικά τα

.
Αποδεικνύουμε ότι:
Λήμμα 2.

και όμοια και για τα άλλα.(εδώ συμβολίζουμε με

τη δύναμη του

ως προς τον

).
Απόδειξη:
Από Μενέλαο στο

με διατέμνουσα την

λαμβάνουμε πως

,

.
Η

διχοτομεί την

οπότε
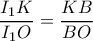
,

και ομοίως

,

.
Από

παίρνουμε

δηλαδή ότι το

είναι η τομή της (εξ. προφανώς) διχοτόμου της

με την

.
Αν

το μέσον του μεγάλου τόξου

,αυτό μας δίνει πως

συνευθειακά.
Από το
Λήμμα 1.,είναι
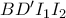
εγγράψιμο οπότε πράγματι έχουμε από δύναμη σημείου το υποζητούμενο.

Εδώ είναι που θα χρειαστούμε για πρώτη φορά το ότι

περιγράψιμο.
Ισχύει το εξής:
Λήμμα 3.

συνευθειακά.
Απόδειξη:
Το

είναι προφανώς παραλληλόγραμμο,οπότε για να δείξουμε πχ. ότι

συνευθειακά,αρκεί από αντίστροφο Θαλή

.
Από γνωστούς τύπους για την εξ.διχοτόμο(-όπως δείχτηκε στο προηγούμενο λήμμα),είναι

ενώ και

.
Αρκεί λοιπόν

που ισχύει καθώς

λόγω του παραλληλογράμμου,

λόγω

(εδώ μόνο χρησιμοποιήθηκε η περιγραψιμότητα) και

.

Ζωγραφίζουμε τώρα τους κύκλους με κέντρα

που είναι ορθογώνιοι στον

.
Επειδή τα κέντρα τους είναι συγγραμικά από
Λήμμα 3,είναι και ομοαξονικοί (αποδεικνύεται απλά με αντιστροφή ως προς τον

).
Θεωρούμε τον κύκλο

.
Από
Λήμμα 2. είναι ορθογώνιος στους

.
Επομένως ,η αντιστροφή ως προς αυτόν ανταλλάζει τα κοινά σημεία των

οπότε το κέντρο του βρίσκεται πάνω στον κοινό ριζικό άξονα.
Έτσι,είναι τελικά ορθογώνιος και στους

.
Αν τέμνει την

για δεύτερη φορά στο

,θα είναι λοιπόν (λόγω ορθογωνιότητας με τον

)

-εκ κατασκευής του

-οπότε από Λήμμα 2 είναι

και το ζητούμενο δείχτηκε..

Σημ.Το αντίστροφο είναι πλέον εύκολο,αν δούμε που χρησιμοποιήθηκε η περιγραψιμότητα...
 εγγεγραμένο σε κύκλο κέντρου
εγγεγραμένο σε κύκλο κέντρου  και περιγεγραμμένο σε κύκλο κέντρου
και περιγεγραμμένο σε κύκλο κέντρου  τετράπλευρο. Να δείξετε ότι τα κέντρα των εγγεγραμμένων κύκλων των τριγώνων
τετράπλευρο. Να δείξετε ότι τα κέντρα των εγγεγραμμένων κύκλων των τριγώνων  και
και  είναι ομοκυκλικά.
είναι ομοκυκλικά. είναι εγγεγραμμένο σε κύκλο κέντρου
είναι εγγεγραμμένο σε κύκλο κέντρου  και τα κέντρα των εγγεγραμμένων κύκλων των τριγώνων
και τα κέντρα των εγγεγραμμένων κύκλων των τριγώνων  και
και  είναι ομοκυκλικά, τότε το τετράπλευρο
είναι ομοκυκλικά, τότε το τετράπλευρο  είναι περιγράψιμο.
είναι περιγράψιμο.
 ,
,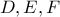 τα μέσα των τόξων
τα μέσα των τόξων  και
και  τυχαίο σημείο στο μικρό τόξο
τυχαίο σημείο στο μικρό τόξο  .
. ,τότε το κέντρο του
,τότε το κέντρο του  βρίσκεται στην
βρίσκεται στην  .
. τα συμμετρικά των
τα συμμετρικά των  προς την
προς την  βρίσκεται πιο κοντά στο
βρίσκεται πιο κοντά στο  από την
από την  .
. οπότε
οπότε  εγγράψιμο.
εγγράψιμο. εγγράψιμο ως τραπέζιο,οπότε
εγγράψιμο ως τραπέζιο,οπότε  ομοκυκλικά και συνεπώς ο
ομοκυκλικά και συνεπώς ο 
 ,
, τα έκκέντρα των
τα έκκέντρα των  και
και  το μέσο του τόξου
το μέσο του τόξου  .
. εγγράψιμο.
εγγράψιμο.
 ,η οποία στέλνει το
,η οποία στέλνει το  -στον
-στον  τις οποίες και ονομάζουμε
τις οποίες και ονομάζουμε  αντίστοιχα.
αντίστοιχα. προκύπτει πως το κέντρο
προκύπτει πως το κέντρο  του
του  βρίσκεται στην
βρίσκεται στην  .
. ) βρίσκεται στον
) βρίσκεται στον  ,το
,το  οπότε εφαρμόζοντας την αντίστροφη ομοιοθεσία (λόγου
οπότε εφαρμόζοντας την αντίστροφη ομοιοθεσία (λόγου  ) παίρνουμε πως το
) παίρνουμε πως το  .
. τα μέσα των
τα μέσα των  αντίστοιχα και
αντίστοιχα και  τα έκκεντρα των
τα έκκεντρα των  (αντίστοιχα).
(αντίστοιχα). είναι συνευθειακές τριάδες.
είναι συνευθειακές τριάδες. και κυκλικά τα
και κυκλικά τα  .
. και όμοια και για τα άλλα.(εδώ συμβολίζουμε με
και όμοια και για τα άλλα.(εδώ συμβολίζουμε με  τη δύναμη του
τη δύναμη του  ).
). με διατέμνουσα την
με διατέμνουσα την  λαμβάνουμε πως
λαμβάνουμε πως  ,
, .
. διχοτομεί την
διχοτομεί την  οπότε
οπότε 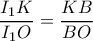 ,
, και ομοίως
και ομοίως  ,
, .
. παίρνουμε
παίρνουμε  δηλαδή ότι το
δηλαδή ότι το  με την
με την  .
. το μέσον του μεγάλου τόξου
το μέσον του μεγάλου τόξου  ,αυτό μας δίνει πως
,αυτό μας δίνει πως  συνευθειακά.
συνευθειακά.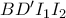 εγγράψιμο οπότε πράγματι έχουμε από δύναμη σημείου το υποζητούμενο.
εγγράψιμο οπότε πράγματι έχουμε από δύναμη σημείου το υποζητούμενο.  συνευθειακά.
συνευθειακά. είναι προφανώς παραλληλόγραμμο,οπότε για να δείξουμε πχ. ότι
είναι προφανώς παραλληλόγραμμο,οπότε για να δείξουμε πχ. ότι  συνευθειακά,αρκεί από αντίστροφο Θαλή
συνευθειακά,αρκεί από αντίστροφο Θαλή  .
. ενώ και
ενώ και  .
. που ισχύει καθώς
που ισχύει καθώς  λόγω του παραλληλογράμμου,
λόγω του παραλληλογράμμου, λόγω
λόγω  (εδώ μόνο χρησιμοποιήθηκε η περιγραψιμότητα) και
(εδώ μόνο χρησιμοποιήθηκε η περιγραψιμότητα) και  .
.  .
. .
. οπότε το κέντρο του βρίσκεται πάνω στον κοινό ριζικό άξονα.
οπότε το κέντρο του βρίσκεται πάνω στον κοινό ριζικό άξονα. .
. για δεύτερη φορά στο
για δεύτερη φορά στο  ,θα είναι λοιπόν (λόγω ορθογωνιότητας με τον
,θα είναι λοιπόν (λόγω ορθογωνιότητας με τον  )
)  -εκ κατασκευής του
-εκ κατασκευής του  και το ζητούμενο δείχτηκε..
και το ζητούμενο δείχτηκε.. 
 σημεία ενός κύκλου
σημεία ενός κύκλου  με κέντρο
με κέντρο  . Τότε ο περιγεγραμμένος κύκλος του τριγώνου
. Τότε ο περιγεγραμμένος κύκλος του τριγώνου  είναι ορθογώνιος προς τον
είναι ορθογώνιος προς τον  θα είναι σε αυτό το μοντέλο ευθεία. Είναι φανερό ότι
θα είναι σε αυτό το μοντέλο ευθεία. Είναι φανερό ότι  . Επομένως αν περάσουμε από το μοντέλο Poincare στο
. Επομένως αν περάσουμε από το μοντέλο Poincare στο  . Σε κύκλους της υπερβολική γεωμετρία αντιστοιχούν ευκλείδειοι κύκλοι στο μοντέλο του Poincare και ελλείψεις, που εφάπτονται του απόλυτου σε δυο σημεία (πραγματικά ή φανταστικά), στο μοντέλο του Klein. Έτσι το αρχικό πρόβλημα μπορεί να αναδιατυπωθεί:
. Σε κύκλους της υπερβολική γεωμετρία αντιστοιχούν ευκλείδειοι κύκλοι στο μοντέλο του Poincare και ελλείψεις, που εφάπτονται του απόλυτου σε δυο σημεία (πραγματικά ή φανταστικά), στο μοντέλο του Klein. Έτσι το αρχικό πρόβλημα μπορεί να αναδιατυπωθεί: ευθεία που τέμνει τον κύκλο
ευθεία που τέμνει τον κύκλο  και
και  (πραγματικά ή φανταστικά). Για τυχόν σημείο
(πραγματικά ή φανταστικά). Για τυχόν σημείο  και την απόστασή του από την ευθεία
και την απόστασή του από την ευθεία  . Τότε ο γεωμετρικός τόπος των σημείων
. Τότε ο γεωμετρικός τόπος των σημείων  , θα είναι κωνική, που εφάπτεται του
, θα είναι κωνική, που εφάπτεται του  ναι είναι αντίστοιχα ανάλογες με τα μήκη αυτών των πλευρών. Έστω
ναι είναι αντίστοιχα ανάλογες με τα μήκη αυτών των πλευρών. Έστω  για τα οποία
για τα οποία  ,
,  . Τότε
. Τότε  ,
,  , δηλαδή
, δηλαδή  βρίσκονται στις προεκτάσεις των πλευρών του παραλληλόγραμμου
βρίσκονται στις προεκτάσεις των πλευρών του παραλληλόγραμμου  . Για αυτό η ευθεία
. Για αυτό η ευθεία  δεν τέμενει το παραλληλόγραμμο. Εξάλλου
δεν τέμενει το παραλληλόγραμμο. Εξάλλου  . Εφόσον
. Εφόσον  ο λόγος
ο λόγος  θα είναι ίδιος με τον παραπάνω. Έτσι ως
θα είναι ίδιος με τον παραπάνω. Έτσι ως  ,
,  ,
,  και
και  είναι ομοκυκλικά αν και μόνο αν το
είναι ομοκυκλικά αν και μόνο αν το