Αφού πρώτα ευχαριστήσω για το ενδιαφέρον και τις ωραίες λύσεις σας,ας ανεβάσω και τη δική μου:
Ας είναι

η τομή των
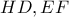
.
Από αντίστροφο Reim's στα ζεύγη

,

έπεται πως τα
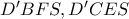
είναι εγγράψιμα.
Επομένως αρκεί να δειχθεί πως

,δηλαδή πως το σημείο

ανήκει στην ισογώνια καμπύλη της μεσοκαθέτου της

.
Αυτή η καμπύλη (στο εξής “Ισοπτική”,αν και ο όρος είναι μάλλον αδόκιμος) είναι γνωστό πως είναι μια ισοσκελής περιγεγραμμένη υπερβολή του

με τις διευθύνσεις των ασυμπτώτων να είναι εκείνες της εσωτερικής/εξωτερικής διχοτόμου της

.
(βλ. πχ.
https://mathematica.gr/forum/viewtopic. ... 81#p306081).
Κάτι που δεν έχει ειπωθεί στο συννημένο είναι πως το μέσο

της

είναι το κέντρο της υπερβολής.
Αυτό δεν είναι δύσκολο:Παρατηρήστε πως το αντιδιαμετρικό του

στον

-έστω

ανήκει στην "Ισοπτική Υπερβολή" του

ως προς

αφού

.
Ως εκτούτου,το μέσον

της

,όντας και μέσον του

είναι κέντρο συμμετρίας της υπερβολής και άρα είναι το κέντρο της...
Γενικότερα,το κέντρο μιας περιγεγραμμένης κωνικής ενός παραλληλογράμμου ταυτίζεται με το κέντρο του παραλληλογράμμου και η απόδειξη είναι απλή(εισάγουμε ένα "phantom point" που υποθέτουμε ότι είναι το κέντρο της κωνικής και καταλήγουμε πως πρέπει να ταυτίζεται με το κέντρο του παραλληλογράμμου).

- Grouplawl.png (35.84 KiB) Προβλήθηκε 961 φορές
Αν ονομάσουμε

την τομή της υπερβολής με την

που δεν είναι το σημείο στο άπειρο με διεύθυνση εκείνη της εξ. διχοτόμου της

(στο εξής

),αρκεί νδο.
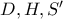
συνευθειακά.
Ας είναι επίσης

η τομή της υπερβολής με την

και

η ασύμπτωτη με διεύθυνση εκείνη της εξ.διχοτόμου της

.
Θεωρούμε τις εκφυλισμένες κυβικές

,
εκ των οποίων οι

τέμνονται στα

(στο

με πολλαπλότητα

διότι η

είναι ασύμπτωτος) και οι

στα

(πάλι στο

με πολλαπλότητα

διότι

).
Συνεπώς,από

,επειδή τα

από τα

σημεια είναι κοινά,θα είναι και τα υπόλοιπα κοινά,δηλαδή

που είναι το ζητούμενο.
Σημ.1.Έχει σημασία το γεγονός ότι η εφαπτομένη της υπερβολής στο

έχει τη διεύθυνση της

για την παραπάνω απόδειξη,καθώς έτσι μπορούμε να θεωρήσουμε το

σαν να είναι "διπλό" σημείο και της

.
Σημ.2.Μπορεί να αποφευχθεί η χρήση του παραπάνω δυνατού θεωρήματος με την εφαρμογή μερικών

.Εξ'άλλου το πρόβλημα κατέληξε να είναι καθαρά προβολικό και επομένως μπορούμε να αγνοήσουμε εντελώς της Γεωμετρικές ιδιότητες των παραπάνω σημείων τομής (πχ.

μέσο της

,

κέντρο του

) και να εργαστούμε μονάχα με τις προβολικές τους (συνευθειακότητες/συντρέχειες/εφάψεις/"ομοκωνικότητες" κλπ.)
 ,
, το ορθόκεντρο και περίκεντρό του,
το ορθόκεντρο και περίκεντρό του, η τομή της εξωτερικής διχοτόμου της
η τομή της εξωτερικής διχοτόμου της  με τον
με τον  ,
, η δεύτερη τομή
η δεύτερη τομή 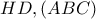 και έστω
και έστω  οι τομές της εκ του
οι τομές της εκ του  παράλληλης στην εξωτερική διχοτόμο της
παράλληλης στην εξωτερική διχοτόμο της  με τις
με τις  .
. διχοτομεί την
διχοτομεί την  .
.
 μέσο της
μέσο της  ,
, το ορθόκεντρο και η διχοτόμος
το ορθόκεντρο και η διχοτόμος  του
του 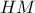 στο
στο  .Από το
.Από το  που τέμνει τις
που τέμνει τις  στα
στα 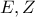 αντίστοιχα.Τότε
αντίστοιχα.Τότε 
 ,
, και
και  το αντιδιαμετρικό του
το αντιδιαμετρικό του  είναι όμοια και
είναι όμοια και  θα είναι
θα είναι 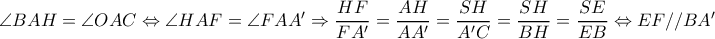
 το περίκεντρο του
το περίκεντρο του  .Από το λήμμα το
.Από το λήμμα το 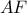 και επειδή
και επειδή  είναι
είναι  .Αν
.Αν 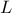 το μέσο του
το μέσο του  τότε τα
τότε τα  θα είναι προφανώς συνευθειακά και θα δείξω ότι είναι και τα
θα είναι προφανώς συνευθειακά και θα δείξω ότι είναι και τα  .Αρκεί
.Αρκεί  το οποίο ισχύει γιατί
το οποίο ισχύει γιατί 
 διχοτόμος της
διχοτόμος της 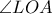 .
. είναι μεσοκάθετος των
είναι μεσοκάθετος των  οπότε εύκολα προκύπτει ότι
οπότε εύκολα προκύπτει ότι  ομοκυκλικά και
ομοκυκλικά και  .
.
 ανήκει στον κύκλο
ανήκει στον κύκλο 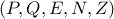 και επειδή
και επειδή  οι γωνίες
οι γωνίες  βαίνουν σε ίσα τόξα άρα είναι ίσες.
βαίνουν σε ίσα τόξα άρα είναι ίσες.
 Το σημείο
Το σημείο  που περιέχει το σημείο
που περιέχει το σημείο  , το μέσον του τόξου, που δεν περιέχει το
, το μέσον του τόξου, που δεν περιέχει το  τέμνει την διχοτόμο
τέμνει την διχοτόμο  της γωνίας
της γωνίας  , στο σημείο έστω
, στο σημείο έστω  και έστω το σημείο
και έστω το σημείο  .
. είναι ρόμβος λόγω
είναι ρόμβος λόγω 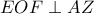 και άρα έχουμε
και άρα έχουμε  .
.
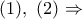
 από όπου προκύπτει και
από όπου προκύπτει και  λόγω συμμετρίας των
λόγω συμμετρίας των  ως προς την
ως προς την  είναι εγγράψιμο σε κύκλο έστω
είναι εγγράψιμο σε κύκλο έστω  με διάμετρο το τμήμα
με διάμετρο το τμήμα  .
. τώρα, προκύπτει ότι το σημείο
τώρα, προκύπτει ότι το σημείο  , σημείο του κύκλου
, σημείο του κύκλου  , είναι και σημείο του κύκλου
, είναι και σημείο του κύκλου  συμπεραίνεται ότι
συμπεραίνεται ότι  και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί. εγγεγραμμένο σε κύκλο
εγγεγραμμένο σε κύκλο  που περιέχει το σημείο
που περιέχει το σημείο  , στο σημείο έστω
, στο σημείο έστω  , το σημείο τομής της πλευράς
, το σημείο τομής της πλευράς  από την μεσοκάθετη ευθεία του
από την μεσοκάθετη ευθεία του 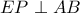
 και
και  και ας είναι
και ας είναι  , τα μέσα των
, τα μέσα των 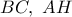 , αντιστοίχως.
, αντιστοίχως. είναι συνευθειακά, λόγω του τραπεζίου
είναι συνευθειακά, λόγω του τραπεζίου  με
με  .
.
 , αρκεί να αποδειχθεί ότι
, αρκεί να αποδειχθεί ότι 
 , αρκεί να αποδειχθεί ότι
, αρκεί να αποδειχθεί ότι 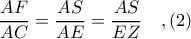 λόγω
λόγω  .
. , λόγω
, λόγω  , σύμφωνα με το
, σύμφωνα με το  λόγω
λόγω  και
και  ( γνωστό αποτέλεσμα ) και
( γνωστό αποτέλεσμα ) και  .
. αρκεί να αποδειχθεί ότι ισχύει
αρκεί να αποδειχθεί ότι ισχύει 
 όμως αληθεύει λόγω των ομοίων ορθογωνίων τριγώνων
όμως αληθεύει λόγω των ομοίων ορθογωνίων τριγώνων  τα οποία έχουν
τα οποία έχουν  και το
και το  η τομή των
η τομή των 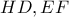 .
. ,
, έπεται πως τα
έπεται πως τα 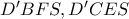 είναι εγγράψιμα.
είναι εγγράψιμα. ,δηλαδή πως το σημείο
,δηλαδή πως το σημείο  ανήκει στην "Ισοπτική Υπερβολή" του
ανήκει στην "Ισοπτική Υπερβολή" του  .
. είναι κέντρο συμμετρίας της υπερβολής και άρα είναι το κέντρο της...
είναι κέντρο συμμετρίας της υπερβολής και άρα είναι το κέντρο της... την τομή της υπερβολής με την
την τομή της υπερβολής με την  που δεν είναι το σημείο στο άπειρο με διεύθυνση εκείνη της εξ. διχοτόμου της
που δεν είναι το σημείο στο άπειρο με διεύθυνση εκείνη της εξ. διχοτόμου της  ),αρκεί νδο.
),αρκεί νδο. 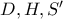 συνευθειακά.
συνευθειακά. η τομή της υπερβολής με την
η τομή της υπερβολής με την  και
και  η ασύμπτωτη με διεύθυνση εκείνη της εξ.διχοτόμου της
η ασύμπτωτη με διεύθυνση εκείνη της εξ.διχοτόμου της  ,
, τέμνονται στα
τέμνονται στα  (στο
(στο  διότι η
διότι η  στα
στα  (πάλι στο
(πάλι στο  ).
). ,επειδή τα
,επειδή τα  από τα
από τα  σημεια είναι κοινά,θα είναι και τα υπόλοιπα κοινά,δηλαδή
σημεια είναι κοινά,θα είναι και τα υπόλοιπα κοινά,δηλαδή  που είναι το ζητούμενο.
που είναι το ζητούμενο. .
. .Εξ'άλλου το πρόβλημα κατέληξε να είναι καθαρά προβολικό και επομένως μπορούμε να αγνοήσουμε εντελώς της Γεωμετρικές ιδιότητες των παραπάνω σημείων τομής (πχ.
.Εξ'άλλου το πρόβλημα κατέληξε να είναι καθαρά προβολικό και επομένως μπορούμε να αγνοήσουμε εντελώς της Γεωμετρικές ιδιότητες των παραπάνω σημείων τομής (πχ.