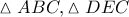 με
με  κατακορυφήν και τον ίδιο παρεγγεγραμμένο κύκλο
κατακορυφήν και τον ίδιο παρεγγεγραμμένο κύκλο  (κέντρου
(κέντρου  ) που αντιστοιχεί στις γωνίες
) που αντιστοιχεί στις γωνίες  . Να δειχθεί ότι η
. Να δειχθεί ότι η  διέρχεται από το κέντρο
διέρχεται από το κέντρο  του εν λόγω κύκλου , όπου
του εν λόγω κύκλου , όπου  τα μέσα των
τα μέσα των  αντίστοιχα.
αντίστοιχα. Στάθης
Συντονιστές: vittasko, silouan, Doloros
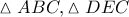 με
με  κατακορυφήν και τον ίδιο παρεγγεγραμμένο κύκλο
κατακορυφήν και τον ίδιο παρεγγεγραμμένο κύκλο  (κέντρου
(κέντρου  ) που αντιστοιχεί στις γωνίες
) που αντιστοιχεί στις γωνίες  . Να δειχθεί ότι η
. Να δειχθεί ότι η  διέρχεται από το κέντρο
διέρχεται από το κέντρο  του εν λόγω κύκλου , όπου
του εν λόγω κύκλου , όπου  τα μέσα των
τα μέσα των  αντίστοιχα.
αντίστοιχα. ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ έγραψε: ↑Πέμ Μάιος 09, 2019 12:05 amΣυνευθειακά.pngΈστω τρίγωναμε
κατακορυφήν και τον ίδιο παρεγγεγραμμένο κύκλο
(κέντρου
) που αντιστοιχεί στις γωνίες
. Να δειχθεί ότι η
διέρχεται από το κέντρο
του εν λόγω κύκλου , όπου
τα μέσα των
αντίστοιχα.
Στάθης
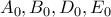 σημεία επαφής των ευθειών
σημεία επαφής των ευθειών  με τον παρεγγεγραμμένο κύκλο αντίστοιχα. Χωρίς βλάβη της γενικότητας μπορούμε να θεωρήσουμε ότι ο κύκλος αυτός είναι ο μοναδιαίος
με τον παρεγγεγραμμένο κύκλο αντίστοιχα. Χωρίς βλάβη της γενικότητας μπορούμε να θεωρήσουμε ότι ο κύκλος αυτός είναι ο μοναδιαίος  του μιγαδικού επιπέδου. Στη συνέχεια με μικρά γράμματα συμβολίζουμε του μιγαδικούς οι εικόνες των οποίων αντιστοιχούν στα αντίστοιχα σημεία με κεφαλαία. Καθένα από τα σημεία
του μιγαδικού επιπέδου. Στη συνέχεια με μικρά γράμματα συμβολίζουμε του μιγαδικούς οι εικόνες των οποίων αντιστοιχούν στα αντίστοιχα σημεία με κεφαλαία. Καθένα από τα σημεία  είναι σημείο τομής εφαπτομένων του μοναδιαίου κύκλου. Οπότε θα έχουμε
είναι σημείο τομής εφαπτομένων του μοναδιαίου κύκλου. Οπότε θα έχουμε


 θα έχουμε
θα έχουμε
 . Άρα τα σημεία
. Άρα τα σημεία  είναι συνευθειακά.
είναι συνευθειακά. η τομή
η τομή  .Ισχύει για κάθε σημείο
.Ισχύει για κάθε σημείο της ευθείας Newton του πλήρους τετραπλεύρου
της ευθείας Newton του πλήρους τετραπλεύρου  πως
πως  και μάλιστα αυτά τα σημεία είναι τα μόνα με αυτή την ιδιότητα (δηλαδή ισχύει και το αντίστροφο).
και μάλιστα αυτά τα σημεία είναι τα μόνα με αυτή την ιδιότητα (δηλαδή ισχύει και το αντίστροφο). στην ευθεία Newton.Μετά δείχνεται απλά με σύγκριση εμβαδών (το μόνο που χρειάζεται είναι πως η διάμεσος διαιρεί το τρίγωνο σε ισεμβαδικά τρίγωνα.).Το αντίστροφο προκύπτει και με άτοπο.
στην ευθεία Newton.Μετά δείχνεται απλά με σύγκριση εμβαδών (το μόνο που χρειάζεται είναι πως η διάμεσος διαιρεί το τρίγωνο σε ισεμβαδικά τρίγωνα.).Το αντίστροφο προκύπτει και με άτοπο. .Είναι και
.Είναι και  λόγω περιγραψιμότητας κι άρα το
λόγω περιγραψιμότητας κι άρα το  ικανοποιεί τη συνθήκη του λήμματος κι άρα βρίσκεται στην ευθεία Newton του
ικανοποιεί τη συνθήκη του λήμματος κι άρα βρίσκεται στην ευθεία Newton του  κλπ.
κλπ. με παρεγγεγραμμένο κύκλο τον
με παρεγγεγραμμένο κύκλο τον  , σύμφωνα με το οποίο η ευθεία που συνδέει τα μέσα των διαγωνίων του
, σύμφωνα με το οποίο η ευθεία που συνδέει τα μέσα των διαγωνίων του 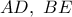 , περνάει από το κέντρο
, περνάει από το κέντρο  του κύκλου
του κύκλου  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες