Με λίγες διαφορές...
Εφόσον το τετράπλευρο είναι αρμονικό, γνωρίζουμε ότι οι διχοτόμοι

και

αντίστοιχα των γωνιών

και

, θα τέμνονται στο σημείο

της διαγωνίου

. Επίσης, το σημείο τομής

των εξωτερικών διχοτόμων των γωνιών
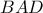
και

θα ανήκει στην ευθεία της διαγωνίου

. Στη συνέχεια, έστω

,

τα σημεία στα οποία οι

και

τέμνουν τις

και

αντίστοιχα. Θα αποδείξουμε ότι η ευθεία

διέρχεται από το σημείο

. Αρκεί,

(Θεώρημα Μενελάου).
Από τα θεωρήματα των διχοτόμων έχουμε

Εφόσον το τετράπλευρο είναι αρμονικό, τότε

Επομένως, το αριστερό μέλος της

, λόγω των

και

γίνεται:

Τώρα, το συμπέρασμα του προβλήματος προκύπτει με εφαρμογή του αντίστροφου του θεωρήματος Desargques στα τρίγωνα

και

. Πράγματι, τα σημεία τομής

,

,

αντίστοιχα των ευθειών
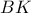
και

,

και

,

και

ανήκουν στην ίδια ευθεία, οπότε οι ευθείες που συνδέουν τις κορυφές

και

,

και

,

και

θα διέρχονται από το ίδιο σημείο. Όμως, το σημείο τομής των

και

είναι το

. Επομένως, και η ευθεία

θα διέρχεται και αυτή από το

, που είναι το αποδεικτέο.

- Line_incen_sol.png (72.94 KiB) Προβλήθηκε 919 φορές
 . Να αποδείξετε ότι η ευθεία που ορίζεται από τα έγκεντρα
. Να αποδείξετε ότι η ευθεία που ορίζεται από τα έγκεντρα  και
και  αντίστοιχα των τριγώνων
αντίστοιχα των τριγώνων  και
και  , διέρχεται από το σημείο τομής
, διέρχεται από το σημείο τομής  των εξωτερικών διχοτόμων των γωνιών
των εξωτερικών διχοτόμων των γωνιών 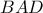 και
και  .
. . Να αποδείξετε ότι η ευθεία που ορίζεται από τα έγκεντρα
. Να αποδείξετε ότι η ευθεία που ορίζεται από τα έγκεντρα  και
και  αντίστοιχα των τριγώνων
αντίστοιχα των τριγώνων  και
και  , διέρχεται από το σημείο τομής
, διέρχεται από το σημείο τομής  των εξωτερικών διχοτόμων των γωνιών
των εξωτερικών διχοτόμων των γωνιών 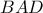 και
και  .
. .(
.( από το αρμονικό τετράπλευρο+θεώρημα εξωτερικής διχοτόμου).
από το αρμονικό τετράπλευρο+θεώρημα εξωτερικής διχοτόμου).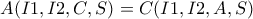 ,γιατί τότε λόγω της κοινής τους ακτίνας τα σημεία τομής των ομόλογων ακτινών θα είναι συνευθειακά.
,γιατί τότε λόγω της κοινής τους ακτίνας τα σημεία τομής των ομόλογων ακτινών θα είναι συνευθειακά. ,δηλαδή αν ορίσω
,δηλαδή αν ορίσω  ,αρκεί
,αρκεί  ,(υπολογίζω τον διπλό λόγο τριγωνομετρικά),δηλαδή
,(υπολογίζω τον διπλό λόγο τριγωνομετρικά),δηλαδή  δηλαδή
δηλαδή  .
. . Iσχύει από νόμο ημιτόνων(
. Iσχύει από νόμο ημιτόνων(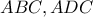 ) και τη σχέση πλευρών του αρμονικού(ίσο γινόμενο απέναντι πλευρών ) ότι
) και τη σχέση πλευρών του αρμονικού(ίσο γινόμενο απέναντι πλευρών ) ότι  οπότε και αρκεί
οπότε και αρκεί  ή
ή  που τελικά καταλήγει στην
που τελικά καταλήγει στην  που ισχύει από ιδιότητες αναλογιών και την
που ισχύει από ιδιότητες αναλογιών και την  .
. στο
στο  . Θα αποδείξουμε πως το
. Θα αποδείξουμε πως το  και όμοια θα ανήκει στην εξωτερική διχοτόμο της
και όμοια θα ανήκει στην εξωτερική διχοτόμο της  .
. .
. να είναι αρμονική.
να είναι αρμονική. ,
,  τέμνονται πάνω στο
τέμνονται πάνω στο  , έστω στο
, έστω στο  . Φέρνουμε τις
. Φέρνουμε τις  και
και  και έστω πως τέμνονται στο
και έστω πως τέμνονται στο  . Η
. Η  τέμνει την
τέμνει την  . Ισχύει από το πλήρες τετράπλευρο
. Ισχύει από το πλήρες τετράπλευρο  ότι η τετράδα
ότι η τετράδα  είναι αρμονική.
είναι αρμονική.  .
. και από
και από  στο
στο 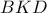 έχουμε ότι
έχουμε ότι  .
.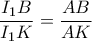 και
και  (θεωρήματα διχοτόμων), οπότε πράγματι
(θεωρήματα διχοτόμων), οπότε πράγματι  .
. και
και  αντίστοιχα των γωνιών
αντίστοιχα των γωνιών  , θα τέμνονται στο σημείο
, θα τέμνονται στο σημείο  της διαγωνίου
της διαγωνίου  και
και  τέμνουν τις
τέμνουν τις  και
και  αντίστοιχα. Θα αποδείξουμε ότι η ευθεία
αντίστοιχα. Θα αποδείξουμε ότι η ευθεία  διέρχεται από το σημείο
διέρχεται από το σημείο  (Θεώρημα Μενελάου).
(Θεώρημα Μενελάου). 

 , λόγω των
, λόγω των  και
και  γίνεται:
γίνεται:
 και
και  . Πράγματι, τα σημεία τομής
. Πράγματι, τα σημεία τομής  ,
,  αντίστοιχα των ευθειών
αντίστοιχα των ευθειών 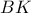 και
και  ,
,  και
και  ανήκουν στην ίδια ευθεία, οπότε οι ευθείες που συνδέουν τις κορυφές
ανήκουν στην ίδια ευθεία, οπότε οι ευθείες που συνδέουν τις κορυφές  και
και  ,
,  θα διέρχεται και αυτή από το
θα διέρχεται και αυτή από το