
Έστω

τα σημεία αντί των

της εκφώνησης αντιστοίχως και έστω τα σημεία

και

.
Στο ορθογώνιο τραπέζιο

, από

και

, σύμφωνα με γνωστό Λήμμα που έχουμε ξαναδεί στο

( Δείτε και
Εδώ ), προκύπτει ότι το σημείο

ανήκει στην ευθεία

και ομοίως για το σημείο

, από

και

.
Από

έχουμε ότι το σημείο

ανήκει επίσης στον κύκλο με διάμετρο

και ομοίως, το σημείο

ανήκει επίσης στον κύκλο με διάμετρο

, από

.
Από το ισοσκελές τραπέζιο
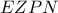
έχουμε ότι οι ως άνω κύκλοι διαμέτρων

τέμνουν την ευθεία

, κοινή μεσοκάθετη των βάσεών του

στα ίδια σημεία, λόγω συμμετρίας ( των διαμέτρων ) ως προς την ευθεία

και επομένως, τα σημεία

ανήκουν και στους δύο ως άνω κύκλους.

- Παρεγγεγραμμένοι κύκλοι και καθετότητα - Απόδειξη της πρότασης.
- f185 t62160(c).png (47.03 KiB) Προβλήθηκε 1255 φορές

Έστω τα σημεία

και

.
Από τα ομοκυκλικά σημεία

τώρα ( ομοίως από τα ομοκυκλικά

), εύκολα προκύπτει ότι

, λόγω των παραλλήλων ευθειών

από τα άκρα της διαμέτρου

ή

του αντίστοιχου κύκλου.
Έχουμε διαμορφώσει έτσι, το τρίγωνο

με

και σύμφωνα με την
Βοηθητική πρόταση που είδαμε στα προηγούμενα, τα σημεία

και

είναι συνευθειακά.
Για την απόδειξη της Βοηθητικής πρότασης , συστήνεται στον αναγνώστη η όμορφη προσέγγιση με Πολικές που μας έδωσε ο Μίνος ( min ) πιο πάνω ( 8η δημοσίευση ).
Έστω το σημείο

και λόγω της συμμετρίας του εξαγώνου

ως προς την ευθεία

, έχουμε ότι τα σημεία

είναι συμμετρικά ως προς την

και άρα, τα τρίγωνα
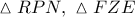
είναι συμμετρικά ως προς την ίδια ευθεία και επομένως, είναι ορθολογικά σύμφωνα με την πρόταση που έχουμε δεί
Εδώ.
Όπως επισημαίνεται από τον
Σταύρο Παπαδόπουλο στην παραπομπή, το κριτήριο για την ορθολογικότητα των τριγώνων
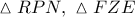
δεν είναι η συμμετρικότητά τους ως προς την ευθεία

αυτή καθεαυτή, αλλά το ότι τα τρίγωνα αυτά είναι όμοια και αντίρροπα μεταξύ τους ( ως ειδική περίπτωση λόγω της συμμετρικότητάς τους ).
Από την ορθολογικότητα των ως άνω τριγώνων τέλος και επειδή το σημείο

ταυτίζεται με το σημείο τομής των δια των κορυφών

του τριγώνου

καθέτων ευθειών, επί των ευθειών των πλευρών

του τριγώνου

αντιστοίχως, συμπεραίνεται ότι η ευθεία

είναι κάθετη επί την

και το ζητούμενο έχει αποδειχθεί.

Η απόδειξη αυτή αφιερώνεται σε ένδειξη τιμής, στον
Μίνο Μαργαρίτη.
Κώστας Βήττας.
 -παρεγγεγραμμένος κύκλος
-παρεγγεγραμμένος κύκλος  δοσμένου τριγώνου
δοσμένου τριγώνου  , εφάπτεται των ευθειών
, εφάπτεται των ευθειών  , στα σημεία
, στα σημεία  αντιστοίχως και ο
αντιστοίχως και ο  -παρεγγεγραμμένος κύκλος του
-παρεγγεγραμμένος κύκλος του  , εφάπτεται των ευθειών
, εφάπτεται των ευθειών  , στα σημεία
, στα σημεία  , αντιστοίχως. Αποδείξτε ότι
, αντιστοίχως. Αποδείξτε ότι  , όπου
, όπου  και
και  , με
, με  το κέντρο του εγγεγραμμένου κύκλου του
το κέντρο του εγγεγραμμένου κύκλου του  .
Κώστας Βήττας.
.
Κώστας Βήττας.
 Έχει δειχθεί ότι
Έχει δειχθεί ότι  και ας είναι
και ας είναι  και
και  και
και  οι ορθές προβολές των
οι ορθές προβολές των 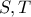 επί τις
επί τις  αντίστοιχα .
αντίστοιχα . για τις ομόλογες διχοτόμους τους
για τις ομόλογες διχοτόμους τους  θα ισχύει:
θα ισχύει:  .
. με
με  (κατακορυφήν) θα έχουμε :
(κατακορυφήν) θα έχουμε :




 θα έχουμε:
θα έχουμε: 




 .
.  θα είναι:
θα είναι: 









 .
. .
.
 .
. και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί. Θα αποδείξουμε πρώτα την ακόλουθη βοηθητική πρόταση:
Θα αποδείξουμε πρώτα την ακόλουθη βοηθητική πρόταση: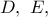 τα σημεία επί της πλευράς του
τα σημεία επί της πλευράς του  ώστε να είναι
ώστε να είναι  και ας είναι το σημείο
και ας είναι το σημείο  μεταξύ των
μεταξύ των  . Οι δια των σημείων
. Οι δια των σημείων  κάθετες ευθείες επί την
κάθετες ευθείες επί την  στα σημεία
στα σημεία  αντιστοίχως και ας είναι
αντιστοίχως και ας είναι  , το συμμετρικό σημείο του
, το συμμετρικό σημείο του  ως προς την ευθεία
ως προς την ευθεία  κάθετη ευθεία επί την
κάθετη ευθεία επί την 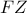 στο σημείο έστω
στο σημείο έστω  . Αποδείξτε ότι τα σημεία
. Αποδείξτε ότι τα σημεία  και
και  είναι συνευθειακά
είναι συνευθειακά συνευθειακά αρκεί, σύμφωνα με το
συνευθειακά αρκεί, σύμφωνα με το 
 στο τραπέζιο
στο τραπέζιο  έχουμε
έχουμε 
 στο τρίγωνο
στο τρίγωνο  έχουμε
έχουμε  όπου
όπου  είναι η προβολή του
είναι η προβολή του  επί της
επί της  στο τρίγωνο
στο τρίγωνο  έχουμε
έχουμε  όπου
όπου  είναι η προβολή του
είναι η προβολή του  επί της
επί της 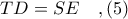
 αρκεί να αποδειχθεί ότι ισχύει
αρκεί να αποδειχθεί ότι ισχύει 
 λόγω
λόγω  .
. αρκεί να αποδειχθεί ότι ισχύει
αρκεί να αποδειχθεί ότι ισχύει 
 και
και 


 αρκεί να αποδειχθεί ότι ισχύει
αρκεί να αποδειχθεί ότι ισχύει  λόγω
λόγω  .
. στα σημεία έστω
στα σημεία έστω  αντιστοίχως και η δια του σημείου
αντιστοίχως και η δια του σημείου 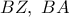 , στα σημεία
, στα σημεία  , αντιστοίχως.
, αντιστοίχως.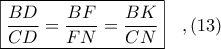
 και
και 


 λόγω
λόγω  .
.
 και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί. όπου
όπου  είναι οι προβολές των σημείων
είναι οι προβολές των σημείων  επί της
επί της  τέμνει τις ευθείες
τέμνει τις ευθείες  στα σημεία έστω
στα σημεία έστω  στα σημεία
στα σημεία  αντιστοίχως.
αντιστοίχως.



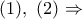

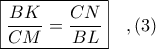 λόγω
λόγω 
 λόγω
λόγω  και
και  λόγω
λόγω  .
.

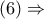


 και το
και το  το ισοτομικό του),η συνέχεια θα είναι απλή.
το ισοτομικό του),η συνέχεια θα είναι απλή. προκύπτουν με παράλληλη προβολή από τα
προκύπτουν με παράλληλη προβολή από τα 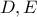 και συνεπώς καθώς κινείται το
και συνεπώς καθώς κινείται το  για τα μεταβλητά
για τα μεταβλητά  έχουν ίσους λόγους,και επειδή όταν το
έχουν ίσους λόγους,και επειδή όταν το 
 στην
στην  και το
και το 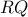 είναι η πολική του
είναι η πολική του  ως προς τον
ως προς τον  (
(
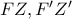 ):Στο πλήρες τετράπλευρο
):Στο πλήρες τετράπλευρο οι διαγώνιοι τέμνονται αρμονικά πράγμα που αναγκάζει το
οι διαγώνιοι τέμνονται αρμονικά πράγμα που αναγκάζει το  .
.
 τα σημεία αντί των
τα σημεία αντί των  της εκφώνησης αντιστοίχως και έστω τα σημεία
της εκφώνησης αντιστοίχως και έστω τα σημεία  και
και  .
. , από
, από  και
και  , σύμφωνα με γνωστό Λήμμα που έχουμε ξαναδεί στο
, σύμφωνα με γνωστό Λήμμα που έχουμε ξαναδεί στο  και ομοίως για το σημείο
και ομοίως για το σημείο  , από
, από  και
και  .
.  έχουμε ότι το σημείο
έχουμε ότι το σημείο  και ομοίως, το σημείο
και ομοίως, το σημείο  , από
, από  .
.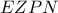 έχουμε ότι οι ως άνω κύκλοι διαμέτρων
έχουμε ότι οι ως άνω κύκλοι διαμέτρων  τέμνουν την ευθεία
τέμνουν την ευθεία  στα ίδια σημεία, λόγω συμμετρίας ( των διαμέτρων ) ως προς την ευθεία
στα ίδια σημεία, λόγω συμμετρίας ( των διαμέτρων ) ως προς την ευθεία  και
και  .
. τώρα ( ομοίως από τα ομοκυκλικά
τώρα ( ομοίως από τα ομοκυκλικά  ), εύκολα προκύπτει ότι
), εύκολα προκύπτει ότι  , λόγω των παραλλήλων ευθειών
, λόγω των παραλλήλων ευθειών  από τα άκρα της διαμέτρου
από τα άκρα της διαμέτρου  με
με  είναι συνευθειακά.
είναι συνευθειακά. και λόγω της συμμετρίας του εξαγώνου
και λόγω της συμμετρίας του εξαγώνου  ως προς την ευθεία
ως προς την ευθεία  , έχουμε ότι τα σημεία
, έχουμε ότι τα σημεία  είναι συμμετρικά ως προς την
είναι συμμετρικά ως προς την 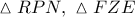 είναι συμμετρικά ως προς την ίδια ευθεία και επομένως, είναι ορθολογικά σύμφωνα με την πρόταση που έχουμε δεί
είναι συμμετρικά ως προς την ίδια ευθεία και επομένως, είναι ορθολογικά σύμφωνα με την πρόταση που έχουμε δεί  του τριγώνου
του τριγώνου  καθέτων ευθειών, επί των ευθειών των πλευρών
καθέτων ευθειών, επί των ευθειών των πλευρών  του τριγώνου
του τριγώνου  αντιστοίχως, συμπεραίνεται ότι η ευθεία
αντιστοίχως, συμπεραίνεται ότι η ευθεία  είναι κάθετη επί την
είναι κάθετη επί την  και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί.