
- orth_tang.png (83.47 KiB) Προβλήθηκε 842 φορές
Έστω

ο περιγεγραμμένος κύκλος του

με κέντρο το

που ανήκει στο ύψος

αυτού του τριγώνου. Τότε,

(εντός εκτός επί τα αυτά μέρη των παραλλήλων

,

που τέμνονται από την

),

(το ύψος

του ισοσκελούς τριγώνου είναι και διχοτόμος).
Επομένως,

, δηλαδή, η ακτίνα

του κύκλου

εφάπτεται του κύκλου

,
οπότε οι δύο κύκλοι είναι ορθογώνιοι, και έστω

το δεύτερο κοινό τους σημείο.
Από τα εγγεγραμμένα τετράπλευρα

και

έχουμε

και

,
οπότε

Από την ομοιότητα των ορθογωνίων τριγώνων

και

έχουμε

Από

και

έχουμε ότι

, δηλαδή η

διχοτόμος της γωνίας

.
Στη συνέχεια, θα αποδείξουμε ότι και ο κύκλοι

και

είναι επίσης ορθογώνιοι.
Αρκεί να αποδείξουμε ότι

[αν δύο σημεία ένός κύκλου (εδώ τα

,

του

) είναι αντίστροφα
ως προς έναν άλλο κύκλο (εδώ του

), τότε οι δύο κύκλοι είναι ορθογώνιοι].
Από την παραλληλία

έχουμε

Από την παραλληλία

έχουμε

Εφόσον τα δεύτερα μέλη των

,

είναι ίσα, τότε

.
Αν τώρα,

το δεύτερο σημείο τομής της ευθείας

με τον κύκλο

, τότε

, και εφόσον
η

διχοτόμος της γωνίας

, τότε ο κύκλος

είναι ένας Απολλώνιος κύκλος, δηλαδή, είναι
ο γεωμετρικός τόπος των σημείων των οποίων ο λόγος των αποστάσεων από τα

και

είναι
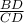
,
οπότε λόγω της

το σημείο

ανήκει στον κύκλο

.
Τώρα το ζητούμενο είναι προφανές, εφόσον οι τρεις κύκλοι διέρχονται από το σημείο

, και οι

,

ορθογώνιοι του

, δηλαδή

(

το κέντρο του

),

.
ΥΓ. Το πρόβλημα αυτό δόθηκε στο διαγωνισμό (τελικό γύρο) που διενεργείται στη Ρωσία προς τιμή του I.F. Sharygin το 2017.
Η παραπάνω λύση είναι περίπου όμοια με την επίσημη υπόδειξη - λύση της επιτροπής. Απλώς, εδώ δεν χρησιμοποιείται ο μετασχηματισμός της σπειροειδούς ομοιότητας.
 ,
,  και στη βάση
και στη βάση  ενός ισοσκελούς τριγώνου
ενός ισοσκελούς τριγώνου  ,
,  ,
,  και
και  έτσι ώστε το
έτσι ώστε το  να είναι παραλληλόγραμμο.
να είναι παραλληλόγραμμο.  το κοινό σημείο των ευθειών
το κοινό σημείο των ευθειών  και
και  , και έστω
, και έστω  ,
,  τα σημεία στα οποία
τα σημεία στα οποία  στο
στο  , τέμνει τις
, τέμνει τις  ,
,  αντίστοιχα. Να αποδείξετε ότι ο κύκλος
αντίστοιχα. Να αποδείξετε ότι ο κύκλος  κέντρου
κέντρου και ακτίνας
και ακτίνας  , εφάπτεται του περιγεγραμμένου κύκλου
, εφάπτεται του περιγεγραμμένου κύκλου  του τριγώνου
του τριγώνου  .
.
 το κέντρου του παραλληλογράμμου
το κέντρου του παραλληλογράμμου  οι ορθές προβολές των
οι ορθές προβολές των  στις ευθείες
στις ευθείες  αντίστοιχα και
αντίστοιχα και  οι ορθές προβολές του
οι ορθές προβολές του  το μέσο της διακέντρου
το μέσο της διακέντρου  των εν λόγω κύκλων.
των εν λόγω κύκλων. 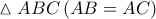 και την κάθετη στην
και την κάθετη στην  είναι ισοσκελές και συνεπώς
είναι ισοσκελές και συνεπώς  .
.  τα μέσα των
τα μέσα των  αντίστοιχα. Και προφανώς (από τα αποστήματα)
αντίστοιχα. Και προφανώς (από τα αποστήματα)  τα μέσα των (χορδών του
τα μέσα των (χορδών του  )
)  αντίστοιχα.
αντίστοιχα.  και ομοίως
και ομοίως  .
. προκύπτει ότι
προκύπτει ότι  .
.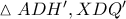

 .
.

 σύμφωνα με το
σύμφωνα με το  .
. 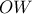 του τραπεζίου
του τραπεζίου  προκύπτει ότι
προκύπτει ότι 

 εφάπτονται εξωτερικά (η διάκεντρός τους ισούται με το άθροισμα των ακτινών τους) και το ζητούμενο έχει αποδειχθεί.
εφάπτονται εξωτερικά (η διάκεντρός τους ισούται με το άθροισμα των ακτινών τους) και το ζητούμενο έχει αποδειχθεί. και της ευθείας
και της ευθείας  δημιουργώντας αντίστοιχα μεγέθη που θα ταυτιστούν τελικά, λόγω του ότι ορίζεται μονοσήμαντα το σημείο
δημιουργώντας αντίστοιχα μεγέθη που θα ταυτιστούν τελικά, λόγω του ότι ορίζεται μονοσήμαντα το σημείο  με αυτά.
με αυτά.  και της ισότητας
και της ισότητας  , ότι το
, ότι το  Με διάμετρο το
Με διάμετρο το  γράφουμε κύκλο που τέμνει τον
γράφουμε κύκλο που τέμνει τον  στο
στο 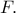 Έστω
Έστω 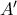 το αντιδιαμετρικό του
το αντιδιαμετρικό του  στον κύκλο
στον κύκλο  του ισοσκελούς τριγώνου
του ισοσκελούς τριγώνου  Τότε,
Τότε,  Αυτό σημαίνει ότι τα σημεία
Αυτό σημαίνει ότι τα σημεία 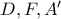 είναι συνευθειακά. Έστω
είναι συνευθειακά. Έστω  η τομή των ημιευθειών
η τομή των ημιευθειών  και
και  η τομή των ημιευθειών
η τομή των ημιευθειών  όπου
όπου  Ο κύκλος
Ο κύκλος  είναι εφαπτόμενος στον κύκλο
είναι εφαπτόμενος στον κύκλο  Η
Η  είναι μεσοκάθετη του
είναι μεσοκάθετη του  και τέμνει την
και τέμνει την  . Επομένως
. Επομένως  ως κάθετες στην ευθεία
ως κάθετες στην ευθεία 


 Τελικά
Τελικά  και
και  Εδώ το πρόβλημα έχει λυθεί.
Εδώ το πρόβλημα έχει λυθεί. 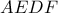 είναι εγγράψιμο.
είναι εγγράψιμο.  είναι ίσο με
είναι ίσο με  , τότε από δύναμη σημείου ξέρουμε πως
, τότε από δύναμη σημείου ξέρουμε πως 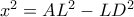 . Άρα αρκεί
. Άρα αρκεί  .
. και πως
και πως  .
. (1).
(1). .
.
 .
. , δηλαδή από την (1) αρκεί
, δηλαδή από την (1) αρκεί  .
. το μέσο του
το μέσο του  που ισχύει λόγω του ότι το τρίγωνο
που ισχύει λόγω του ότι το τρίγωνο  είναι ορθογώνιο.
είναι ορθογώνιο. (νομίζω πως υπάρχει).
(νομίζω πως υπάρχει). εφάπτεται στην τετράδα κύκλων
εφάπτεται στην τετράδα κύκλων  , όπου οι κύκλοι
, όπου οι κύκλοι  είναι μοναδιαία σημεία!
είναι μοναδιαία σημεία! αντίστοιχα.
αντίστοιχα. , άρα αρκεί να ικανοποιείται η συνθήκη
, άρα αρκεί να ικανοποιείται η συνθήκη  για να εφάπτεται και με τον
για να εφάπτεται και με τον  .
. είναι το μήκος της κοινής εφαπτομένης από τους κύκλους
είναι το μήκος της κοινής εφαπτομένης από τους κύκλους  , τότε πρέπει:
, τότε πρέπει: .
.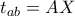 ,
,  ,
,  ,
,  ,
,  (από την (2)),
(από την (2)),  .
. (3)
(3) 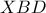 και
και  είναι όμοια αφού έχουν μια οξεία γωνία ίση. Άρα εύκολα προκύπτει πως
είναι όμοια αφού έχουν μια οξεία γωνία ίση. Άρα εύκολα προκύπτει πως  , δηλαδή το τρίγωνο
, δηλαδή το τρίγωνο  είναι ισοσκελές, με
είναι ισοσκελές, με  .
.
 .
. το μέσο του
το μέσο του  . Θέλουμε να αποδείξουμε πως:
. Θέλουμε να αποδείξουμε πως: που ισχύει από θεώρημα Θαλή λόγω των παράλληλων ευθειών
που ισχύει από θεώρημα Θαλή λόγω των παράλληλων ευθειών  και
και 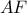 .
.  ο περιγεγραμμένος κύκλος του
ο περιγεγραμμένος κύκλος του  με κέντρο το
με κέντρο το 
 (εντός εκτός επί τα αυτά μέρη των παραλλήλων
(εντός εκτός επί τα αυτά μέρη των παραλλήλων  που τέμνονται από την
που τέμνονται από την  (το ύψος
(το ύψος  , δηλαδή, η ακτίνα
, δηλαδή, η ακτίνα  του κύκλου
του κύκλου  και
και  έχουμε
έχουμε και
και ,
,
 και
και  έχουμε
έχουμε 
 και
και  έχουμε ότι
έχουμε ότι  , δηλαδή η
, δηλαδή η  διχοτόμος της γωνίας
διχοτόμος της γωνίας  .
. [αν δύο σημεία ένός κύκλου (εδώ τα
[αν δύο σημεία ένός κύκλου (εδώ τα  ,
,  του
του  έχουμε
έχουμε 
 έχουμε
έχουμε 
 ,
,  είναι ίσα, τότε
είναι ίσα, τότε  .
.  , και εφόσον
, και εφόσον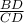 ,
, (
( το κέντρο του
το κέντρο του  .
.