Ωραίες λύσεις!

Μια διαφορετική αντιμετώπιση:

- Ίσα τμήματα! (2) sol.png (46.72 KiB) Προβλήθηκε 1001 φορές
Θα αποδείξουμε αρχικά ένα "λήμμα":
Έχουμε το εγγράψιμο, σε κύκλο με κέντρο

, τετράπλευρο

και έστω

είναι το συμμετρικό του ως προς το

. Έστω

η τομή της

και

και

η τομή της

και

. Να αποδειχθεί πως

είναι συνευθειακά και πως

.
Έστω

η τομή του

και του

. Από

για το μη κυρτό αλλά εγγράψιμο σε κύκλο εξάγωνο

έχουμε πως το σημείο τομής των

και

, δηλαδή το

, το σημείο τομής των

και

, δηλαδή το

, το σημείο τομής των

και

, δηλαδή το

, είναι συνευθειακά σημεία.
Από

όμως για το μη κυρτό αλλά εγγράψιμο σε κύκλο εξάγωνο

έχουμε πως το σημείο τομής των
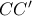
και

, δηλαδή το

, το σημείο τομής των

και

, δηλαδή το

, το σημείο τομής των

και

, δηλαδή το

, είναι συνευθειακά σημεία.
Έπεται λοιπόν από τις δύο παραπάνω συνευθειακότητες ότι τα σημεία

είναι συνευθειακά.
Ακόμα έχουμε τώρα πως τα τετράπλευρα

και

είναι όμοια. Επομένως έχουμε πως

. Από εγγεγραμμένες όμως έχουμε πως

. Άρα

και αφού

έχουμε πως

.
Ας γυρίσουμε πίσω στο αρχικό μας πρόβλημα. Από το προηγούμενο λήμμα αποδείξαμε πως τα σημεία

είναι συνευθειακά, που σημαίνει πως τα σημεία που η

τέμνει τις

θα είναι τα

του λήμματος, με άλλα λόγια πράγματι θα ισχύει πως

.
 και σημείο
και σημείο  στο εξωτερικό του. Φέρνουμε τις δύο τυχαίες τέμνουσες
στο εξωτερικό του. Φέρνουμε τις δύο τυχαίες τέμνουσες 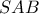 και
και  στον κύκλο. Έστω
στον κύκλο. Έστω  το αντιδιαμετρικό του
το αντιδιαμετρικό του  και
και  του
του  στον κύκλο. Έστω ότι οι
στον κύκλο. Έστω ότι οι 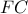 και
και  τέμνουν την
τέμνουν την  στα
στα  αντίστοιχα. Να αποδειχθεί πως
αντίστοιχα. Να αποδειχθεί πως 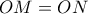 .
.
 (
( ),τότε τα
),τότε τα  είναι συνευθειακά.Δηλαδή θα δείξω ότι
είναι συνευθειακά.Δηλαδή θα δείξω ότι  με
με  τομή των
τομή των  .Με
.Με  τομή
τομή  .Με κατάλληλους νόμους ημιτόνων στα
.Με κατάλληλους νόμους ημιτόνων στα  παίρνουμε
παίρνουμε  (λόγω καθετοτήτων).Ομοίως,
(λόγω καθετοτήτων).Ομοίως,  ,
, και αντικαθιστώντας στην
και αντικαθιστώντας στην  αρκεί να δείξω ότι
αρκεί να δείξω ότι  ,από το οποίο,απλοποιώντας μένει
,από το οποίο,απλοποιώντας μένει  που ισχύει από τα όμοια τρίγωνα
που ισχύει από τα όμοια τρίγωνα  .
. έχουμε
έχουμε

 (1), ή ισοδύναμα
(1), ή ισοδύναμα

 (2)
(2) είναι το σημείο τομής των χορδών που ορίζονται από τους μιγαδικούς
είναι το σημείο τομής των χορδών που ορίζονται από τους μιγαδικούς  και
και  καθώς και από τους μιγαδικούς
καθώς και από τους μιγαδικούς  και
και  . Οπότε για τον μιγαδικό
. Οπότε για τον μιγαδικό  θα ισχύει
θα ισχύει


 και έστω
και έστω  είναι το συμμετρικό του ως προς το
είναι το συμμετρικό του ως προς το  η τομή της
η τομή της  και
και  και
και  η τομή της
η τομή της  και
και  . Να αποδειχθεί πως
. Να αποδειχθεί πως  είναι συνευθειακά και πως
είναι συνευθειακά και πως  .
. και του
και του  . Από
. Από  για το μη κυρτό αλλά εγγράψιμο σε κύκλο εξάγωνο
για το μη κυρτό αλλά εγγράψιμο σε κύκλο εξάγωνο  έχουμε πως το σημείο τομής των
έχουμε πως το σημείο τομής των  και
και  , δηλαδή το
, δηλαδή το  και
και  , δηλαδή το
, δηλαδή το  έχουμε πως το σημείο τομής των
έχουμε πως το σημείο τομής των 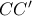 και
και  , δηλαδή το
, δηλαδή το  και
και  , δηλαδή το
, δηλαδή το  είναι συνευθειακά.
είναι συνευθειακά.  . Από εγγεγραμμένες όμως έχουμε πως
. Από εγγεγραμμένες όμως έχουμε πως  . Άρα
. Άρα  και αφού
και αφού  έχουμε πως
έχουμε πως  θα είναι τα
θα είναι τα