 και σημείο
και σημείο  στο εξωτερικό του. Φέρνουμε μια εφαπτόμενη
στο εξωτερικό του. Φέρνουμε μια εφαπτόμενη  και μια τέμνουσα
και μια τέμνουσα  στον κύκλο. Έστω
στον κύκλο. Έστω  το αντιδιαμετρικό του
το αντιδιαμετρικό του  στον κύκλο. Έστω ότι οι
στον κύκλο. Έστω ότι οι  τέμνουν την
τέμνουν την  στα
στα  αντίστοιχα. Να αποδειχθεί πως
αντίστοιχα. Να αποδειχθεί πως 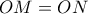 .
.
Συντονιστές: vittasko, silouan, Doloros
 και σημείο
και σημείο  στο εξωτερικό του. Φέρνουμε μια εφαπτόμενη
στο εξωτερικό του. Φέρνουμε μια εφαπτόμενη  και μια τέμνουσα
και μια τέμνουσα  στον κύκλο. Έστω
στον κύκλο. Έστω  το αντιδιαμετρικό του
το αντιδιαμετρικό του  στον κύκλο. Έστω ότι οι
στον κύκλο. Έστω ότι οι  τέμνουν την
τέμνουν την  στα
στα  αντίστοιχα. Να αποδειχθεί πως
αντίστοιχα. Να αποδειχθεί πως 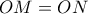 .
.
 την τομή της δεύτερης εφαπτόμενης του
την τομή της δεύτερης εφαπτόμενης του  με τον κύκλο βρίσκουμε ότι
με τον κύκλο βρίσκουμε ότι  .Παίρνω τώρα τομή
.Παίρνω τώρα τομή  έστω
έστω  και
και  τομή
τομή  .Θα αποδείξω ότι η
.Θα αποδείξω ότι η  είναι αρμονική και θα έχω τελειώσει.Με
είναι αρμονική και θα έχω τελειώσει.Με  την τομή των εφαπτόμενων στα
την τομή των εφαπτόμενων στα 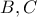 και
και  την τομή των
την τομή των  ,λόγω του ότι τα
,λόγω του ότι τα  ανήκουν στην πολική του
ανήκουν στην πολική του  αρκεί να βγάλω και το
αρκεί να βγάλω και το  συνευθειακό(θα ανήκει τότε στην πολική του
συνευθειακό(θα ανήκει τότε στην πολική του  ).Λόγω πολικών είναι τα
).Λόγω πολικών είναι τα  συνευθειακά οπότε το ζητούμενο έπεται από Pascal στο
συνευθειακά οπότε το ζητούμενο έπεται από Pascal στο  ...Το σχήμα μαζί με διορθώσεις(ίσως) αύριο...
...Το σχήμα μαζί με διορθώσεις(ίσως) αύριο...Διονύσιος Αδαμόπουλος έγραψε: ↑Κυρ Σεπ 17, 2017 4:05 pmΈστω κύκλος με κέντροκαι σημείο
στο εξωτερικό του. Φέρνουμε μια εφαπτόμενη
και μια τέμνουσα
στον κύκλο. Έστω
το αντιδιαμετρικό του
στον κύκλο. Έστω ότι οι
τέμνουν την
στα
αντίστοιχα. Να αποδειχθεί πως
.
Ίσα τμήματα!.png
 σημεία του μοναδιαίου κύκλου
σημεία του μοναδιαίου κύκλου  τότε
τότε δίνεται από τον μιγαδικό
δίνεται από τον μιγαδικό  .
. δίνεται από τον μιγαδικό
δίνεται από τον μιγαδικό  .
. της ευθείας που ορίζουν τα
της ευθείας που ορίζουν τα  ικανοποιεί την σχέση
ικανοποιεί την σχέση  .
. να βρίσκονται στον πραγματικό άξονα.
να βρίσκονται στον πραγματικό άξονα.  βρίσκουμε
βρίσκουμε  (1),
(1), αντιστοιχεί στον μιγαδικό
αντιστοιχεί στον μιγαδικό  .
.  βρίσκουμε
βρίσκουμε  (2).
(2). ή ισόδύναμα
ή ισόδύναμα 
 (3).
(3). έχουμε
έχουμε  (4), αφού
(4), αφού  και το σημείο
και το σημείο  είναι το σημείο τομής των εφαπτομένων από το
είναι το σημείο τομής των εφαπτομένων από το  και από το συζηγές του
και από το συζηγές του 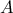 .
. ικανοποιεί την σχέση
ικανοποιεί την σχέση  και λόγω της (4) γίνεται
και λόγω της (4) γίνεται 
 κατά μέλη βρίσκουμε
κατά μέλη βρίσκουμε  και εφόσον
και εφόσον  γίνεται
γίνεται
 ισαπέχουν από το
ισαπέχουν από το  .
.ΑνΔιονύσιος Αδαμόπουλος έγραψε: ↑Κυρ Σεπ 17, 2017 4:05 pmΈστω κύκλος με κέντροκαι σημείο
στο εξωτερικό του. Φέρνουμε μια εφαπτόμενη
και μια τέμνουσα
στον κύκλο. Έστω
το αντιδιαμετρικό του
στον κύκλο. Έστω ότι οι
τέμνουν την
στα
αντίστοιχα. Να αποδειχθεί πως
.
 το δεύτερο εφαπτομενικό τμήμα (εκτός του
το δεύτερο εφαπτομενικό τμήμα (εκτός του  τότε
τότε  μεσοκάθετη της
μεσοκάθετη της  .Από το αρμονικό τετράπλευρο
.Από το αρμονικό τετράπλευρο  προκύπτει ότι η δέσμη
προκύπτει ότι η δέσμη  είναι αρμονική και με
είναι αρμονική και με  το μέσο της
το μέσο της  και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες