 εφάπτεται στις πλευρές
εφάπτεται στις πλευρές  στα
στα 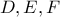 αντίστοιχα και επανατέμνει την
αντίστοιχα και επανατέμνει την  στο
στο 
Ο κύκλος που διέρχεται από τα σημεία
 τέμνει την
τέμνει την  στο
στο  και η
και η  την
την  στο
στο  Να δείξετε ότι
Να δείξετε ότι 
Συντονιστές: vittasko, silouan, Doloros
 εφάπτεται στις πλευρές
εφάπτεται στις πλευρές  στα
στα 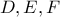 αντίστοιχα και επανατέμνει την
αντίστοιχα και επανατέμνει την  στο
στο 
 τέμνει την
τέμνει την  στο
στο  και η
και η  την
την  στο
στο  Να δείξετε ότι
Να δείξετε ότι 
Έστωgeorge visvikis έγραψε:Ο έγκυκλος τριγώνουεφάπτεται στις πλευρές
στα
αντίστοιχα και επανατέμνει την
στο
Ο κύκλος που διέρχεται από τα σημεία
τέμνει την
στο
και η
την
στο
Να δείξετε ότι
 το σημείο Gergonne (εύκολη απόδειξη με το θεώρημα του Ceva).
το σημείο Gergonne (εύκολη απόδειξη με το θεώρημα του Ceva).  Από το Θεώρημα του Μενελάου στο τρίγωνο
Από το Θεώρημα του Μενελάου στο τρίγωνο  με διατέμνουσα την
με διατέμνουσα την  έχουμε:
έχουμε:  .
. και ας είναι
και ας είναι  το σημείο τομής της εκ του
το σημείο τομής της εκ του  παραλλήλου προς την
παραλλήλου προς την  με την
με την 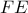 .
. 
 .
. (δηλαδή η σειρά
(δηλαδή η σειρά  είναι αρμονική).
είναι αρμονική). και έστω
και έστω  .
.
 Από το θεώρημα του Pascal στο εκφυλισμένο εγγεγραμμένο στον
Από το θεώρημα του Pascal στο εκφυλισμένο εγγεγραμμένο στον  κυρτό εξάγωνο
κυρτό εξάγωνο  προκύπτει ότι τα σημεία
προκύπτει ότι τα σημεία  (σημεία τομής των απέναντι πλευρών του) είναι συνευθειακά.
(σημεία τομής των απέναντι πλευρών του) είναι συνευθειακά. μη κυρτό εξάγωνο
μη κυρτό εξάγωνο 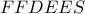 προκύπτει ότι τα σημεία
προκύπτει ότι τα σημεία  (σημεία τομής των απέναντι πλευρών του) είναι συνευθειακά.
(σημεία τομής των απέναντι πλευρών του) είναι συνευθειακά.  εγγεγραμμένο στον κύκλο
εγγεγραμμένο στον κύκλο  (
( εφαπτομενικά τμήματα και
εφαπτομενικά τμήματα και  τέμνουσα του
τέμνουσα του  ) για το
) για το  προκύπτει ότι η δέσμη
προκύπτει ότι η δέσμη  είναι αρμονική και επομένως η σειρά
είναι αρμονική και επομένως η σειρά  είναι αρμονική.
είναι αρμονική.  τότε από το πλήρες τετράπλευρο
τότε από το πλήρες τετράπλευρο  προκύπτει ότι η διαγώνιός του
προκύπτει ότι η διαγώνιός του  διέρχεται από το αρμονικό συζυγές του
διέρχεται από το αρμονικό συζυγές του  ως προς τα
ως προς τα  δηλαδή από το σημείο
δηλαδή από το σημείο  (αφού
(αφού  είναι αρμονική) (κάθε διαγώνιος πλήρους τετραπλεύρου διαιρείται αρμονικά από τις άλλες δύο) δηλαδή τα σημεία
είναι αρμονική) (κάθε διαγώνιος πλήρους τετραπλεύρου διαιρείται αρμονικά από τις άλλες δύο) δηλαδή τα σημεία 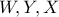 είναι συνευθειακά.
είναι συνευθειακά. μη κυρτό εξάγωνο
μη κυρτό εξάγωνο  προκύπτει ότι τα σημεία
προκύπτει ότι τα σημεία  (σημεία τομής των απέναντι πλευρών του) είναι συνευθειακά.
(σημεία τομής των απέναντι πλευρών του) είναι συνευθειακά. προκύπτει ότι τα σημεία
προκύπτει ότι τα σημεία  είναι συνευθειακά.
είναι συνευθειακά.  Με
Με  αρμονική σειρά προκύπτει ότι και η δέσμη
αρμονική σειρά προκύπτει ότι και η δέσμη  είναι αρμονική και επομένως και η σειρά
είναι αρμονική και επομένως και η σειρά  είναι αρμονική οπότε και η δέσμη
είναι αρμονική οπότε και η δέσμη 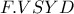 είναι αρμονική δηλαδή η δέσμη
είναι αρμονική δηλαδή η δέσμη  (ταυτίζεται με τη δέσμη
(ταυτίζεται με τη δέσμη 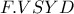 ) είναι αρμονική.
) είναι αρμονική.
 .
. με
με 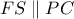 προκύπτει ότι
προκύπτει ότι  είναι το μέσο της
είναι το μέσο της 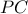 .
.


 και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί.Και θα κέρδιζες το στοίχημα! Οι λύσεις του Στάθη είναι μοναδικέςvittasko έγραψε:...ΥΓ. Θα είναι μεγάλη έκπληξη για μένα, εάν αυτή η απόδειξη είναι γνωστή. Θα στοιχημάτιζα ότι αυτό δεν ισχύει.
 Έστω τα σημεία
Έστω τα σημεία  και
και  .
. , ταυτίζεται με την Πολική ευθεία του σημείου
, ταυτίζεται με την Πολική ευθεία του σημείου  ως προς τον κύκλο
ως προς τον κύκλο  και άρα, το τετράπλευρο
και άρα, το τετράπλευρο  είναι αρμονικό, όπου
είναι αρμονικό, όπου  και επομένως, η δέσμη
και επομένως, η δέσμη  είναι αρμονική.
είναι αρμονική.  και άρα, η σημειοσειρά
και άρα, η σημειοσειρά  είναι αρμονική και επομένως ισχύει
είναι αρμονική και επομένως ισχύει 
 Έστω τα σημεία
Έστω τα σημεία  και
και  .
. ανήκει στην ευθεία
ανήκει στην ευθεία 
 = την Πολική ευθεία του σημείου
= την Πολική ευθεία του σημείου  ως προς τον κύκλο
ως προς τον κύκλο 
 , γιατί το σημείο
, γιατί το σημείο  ανήκει στην Πολική ευθεία του σημείου
ανήκει στην Πολική ευθεία του σημείου  ως προς τον ίδιο κύκλο, λόγω
ως προς τον ίδιο κύκλο, λόγω  .
. ταυτίζεται με την Πολική ευθεία του σημείου
ταυτίζεται με την Πολική ευθεία του σημείου  ως προς τον κύκλο
ως προς τον κύκλο  και άρα, το τετράπλευρο
και άρα, το τετράπλευρο  είναι αρμονικό και επομένως, η δέσμη
είναι αρμονικό και επομένως, η δέσμη  είναι αρμονική.
είναι αρμονική. τώρα, όπου
τώρα, όπου  , είναι αρμονική και άρα, η δέσμη
, είναι αρμονική και άρα, η δέσμη  είναι αρμονική.
είναι αρμονική.
 Από τα εγγράψιμα τετράπλευρα
Από τα εγγράψιμα τετράπλευρα  έχουμε
έχουμε 
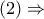

 τώρα, τέμνει την αρμονική δέσμη
τώρα, τέμνει την αρμονική δέσμη  και από
και από  , προκύπτει
, προκύπτει 
 , με το σημείο
, με το σημείο  ως το μέσον του
ως το μέσον του 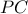 , εύκολα αποδεικνύεται ότι ισχύει
, εύκολα αποδεικνύεται ότι ισχύει 
 και
και 

 .
. με διατέμνουσα την
με διατέμνουσα την  , σύμφωνα με το Θεώρημα Μενελάου, ισχύει
, σύμφωνα με το Θεώρημα Μενελάου, ισχύει 
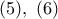 και
και  και
και 
 και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί. είναι ομοκυκλικά
είναι ομοκυκλικά , δείξτε ότι η
, δείξτε ότι η  διχοτομεί την
διχοτομεί την 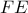
sakis1963 έγραψε:Αφού υποβάλλω τα σέβη μου στους δυο "γίγαντες της Γεωμετρίας" Στάθη και Κώστα, να θέσω δυο πρόσθετα ερωτήματα στο ωραιότατο θέμα του φίλου Γιώργου.
Στο σχήμα του Κώστα
α. Δείξτε ότι τα σημείαείναι ομοκυκλικά
β. Αν, δείξτε ότι η
διχοτομεί την
 α) Είναι
α) Είναι 
 ομοκυκλικά.
ομοκυκλικά. β) Εστω
β) Εστω 
 .
.  ,
, 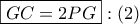 και
και  το μέσο της
το μέσο της 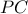 .
. μέσο της
μέσο της  .
. Εχουμε:
Εχουμε: 
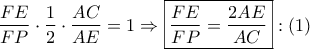 και
και 
 .
. Επίσης
Επίσης 



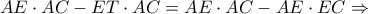
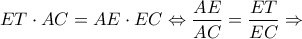

 το μέσο της
το μέσο της  και όλα τα επι πλέον ερωτήματα έχουν αποδειχθεί.
και όλα τα επι πλέον ερωτήματα έχουν αποδειχθεί. και
και  τα σημεία επαφής του εγγεγραμμένου κύκλου ενός τριγώνου
τα σημεία επαφής του εγγεγραμμένου κύκλου ενός τριγώνου  με τις πλευρές του
με τις πλευρές του  και
και 
 το σημείο τομής της διχοτόμου της γωνίας
το σημείο τομής της διχοτόμου της γωνίας  με τη
με τη  , τότε
, τότε  .
. ανήκει στην ευθεία που διέρχεται από τα μέσα των πλευρών
ανήκει στην ευθεία που διέρχεται από τα μέσα των πλευρών  και
και  του τριγώνου
του τριγώνου  .
. το συμμετρικό του
το συμμετρικό του  ως προς τη διχοτόμο
ως προς τη διχοτόμο  , τότε το τρίγωνο
, τότε το τρίγωνο  είναι
είναι  , θα είναι
, θα είναι  .
.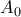 ,
, 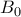 τα μέσα των
τα μέσα των  ,
,  αντίστοιχα, τότε
αντίστοιχα, τότε  (λήμμα, (b)) και αν
(λήμμα, (b)) και αν  , τότε το
, τότε το  είναι
είναι  το κέντρο του,
το κέντρο του,  , και
, και  . Το
. Το  προφανώς μέσο του
προφανώς μέσο του  και
και  . Επομένως,
. Επομένως,  .
. ταυτίζεται με το σημείο
ταυτίζεται με το σημείο  της εκφώνησης του προβλήματος. Αρκεί
της εκφώνησης του προβλήματος. Αρκεί  είναι εγγράψιμο, ή ισοδύναμα
είναι εγγράψιμο, ή ισοδύναμα  .
. ,
,  ,
,  ,
,  ,
,  ,
,  ανήκουν στον κύκλο διαμέτρου
ανήκουν στον κύκλο διαμέτρου 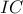 . Επομένως,
. Επομένως,  .
.  . Ως εκ τούτου,
. Ως εκ τούτου, 
 (
( το μέσο του
το μέσο του 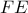 ) τέμνει την
) τέμνει την  στο σημείο
στο σημείο  . Εφόσον
. Εφόσον  , τότε
, τότε  .
. είναι αρμονικό. Επομένως, η
είναι αρμονικό. Επομένως, η 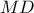 συμμετροδιάμεσος του τριγώνου
συμμετροδιάμεσος του τριγώνου  , οπότε
, οπότε  . Από τις
. Από τις  ,
,  έχουμε
έχουμε  , δηλαδή, το τετράπλευρο
, δηλαδή, το τετράπλευρο 
 .
.  , εφόσον τότε
, εφόσον τότε  , που είναι το αποδεικτέο
, που είναι το αποδεικτέο  .
.  και
και 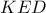 είναι όμοια. Πράγματι,
είναι όμοια. Πράγματι,  (λόγω της
(λόγω της  ), και
), και  (εφόσον η
(εφόσον η  συμμετροδιάμεσος του τριγώνου
συμμετροδιάμεσος του τριγώνου  ).
).  . Επίσης, εφόσον
. Επίσης, εφόσον  , τότε
, τότε  . Με διαίρεση κατά μέλη των
. Με διαίρεση κατά μέλη των  ,
,  έχουμε
έχουμε  (λόγω της
(λόγω της  ).
).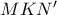 και
και  είναι όμοια, οπότε τώρα προκύπτει το αποδεικτέο
είναι όμοια, οπότε τώρα προκύπτει το αποδεικτέο  που σημαίνει ότι
που σημαίνει ότι  .
. ανήκει επίσης και στον κύκλο
ανήκει επίσης και στον κύκλο  , δηλαδή, ταυτίζεται με το σημείο
, δηλαδή, ταυτίζεται με το σημείο  . Επομένως, το ερώτημα β έχει απαντηθεί.
. Επομένως, το ερώτημα β έχει απαντηθεί. .
. με διατέμνουσα
με διατέμνουσα  κι επEιδή
κι επEιδή  είναι
είναι 
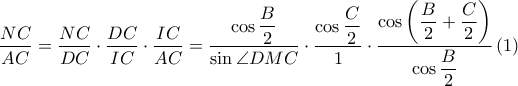


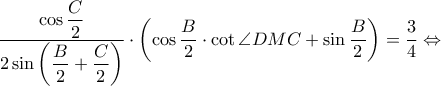

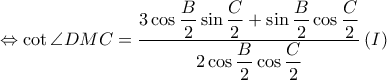
 (too easy με ν. ημιτόνων)
(too easy με ν. ημιτόνων)





 θα λάβουμε:
θα λάβουμε:![\displaystyle \frac{FT}{TE}\cdot \frac{\sin \angle FTN}{\sin \angle ETN}=\frac{\displaystyle 2\cos \frac{A}{2}}{\displaystyle \sin \left ( \frac{A}
{2}+\frac{B}{2} \right )}\cdot \left [ \frac{\displaystyle \sin \left ( \frac{A}{2}-\frac{B}{2} \right )}{\displaystyle 2\cos \frac{A}{2}}+\frac{\displaystyle 2\cos \frac{A}{2}\sin \frac{B}{2}}{\displaystyle 2\cos \frac{A}{2}} \right ]=1 \displaystyle \frac{FT}{TE}\cdot \frac{\sin \angle FTN}{\sin \angle ETN}=\frac{\displaystyle 2\cos \frac{A}{2}}{\displaystyle \sin \left ( \frac{A}
{2}+\frac{B}{2} \right )}\cdot \left [ \frac{\displaystyle \sin \left ( \frac{A}{2}-\frac{B}{2} \right )}{\displaystyle 2\cos \frac{A}{2}}+\frac{\displaystyle 2\cos \frac{A}{2}\sin \frac{B}{2}}{\displaystyle 2\cos \frac{A}{2}} \right ]=1](/forum/ext/geomar/texintegr/latexrender/pictures/5bfa5bbc946d590489fa1b12e40f919b.png)
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες