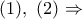Απαιτητική αυτή η κορυφή παραλληλογράμμου, ή όπως λέει και ο φίλτατος
Νίκος Φραγκάκης, ο
Στάθης σε "δαιμονιώδη φόρμα".
Θα αποδειχθεί το ζητούμενο, αφού πρώτα κατασκευαστεί το σχήμα με τρόπο που διευκολύνει την τεκμηρίωση.

Έστω

, τα ύψη του δοσμένου τριγώνου

, με ορθόκεντρο το σημείο έστω

και ας είναι

, τα μέσα των

, αντιστοίχως.
Έστω

, τα μέσα των

αντιστοίχως και από τα εγγράψιμα τετράπλευρα

έχουμε αντιστοίχως,

και

Από

, προκύπτει ότι τα σημεία

είναι συνευθειακά και ας είναι

, το σημείο στην προέκταση του

προς το μέρος του

, ώστε να είναι

Έστω

, οι προβολές του σημείου

επί των

αντιστοίχως και ας είναι

, το σημείο ώστε το

να είναι παραλλήλόγραμμο.
Ως ισοδύναμο ζητούμενο, αρκεί να αποδειχθεί ότι ισχύει

, όπου

.

- Η τέταρτη κορυφή παραλληλογράμμου, σε τροχιά συνευθειακότητας.
- f=185_t=57444.png (41.32 KiB) Προβλήθηκε 952 φορές

Έστω

, οι προβολές του

επί των

αντιστοίχως και ας είναι

, το σημείο ώστε το

να είναι παραλληλόγραμμο.
Από τα συνευθειακά σημεία

, σύμφωνα με το
Θεώρημα των Αναλόγων Διαιρέσεων , έχουμε


οι προβολές τριών συνευθειακών σημείων, επί δύο τεμνόμενων ευθειών, ορίζουν τμήματα με ίσους λόγους

Από

και

τώρα, σύμφωνα με το ίδιο θεώρημα ( γενίκευση ), προκύπτει ότι τα σημεία

είναι συνευθειακά.

Εάν δύο δέσμες των τριών παραλλήλων ευθειών με ίσους λόγους τέμνονται, τα σημεία τομής των ομολόγων ευθειών τους είναι συνευθειακά


Σύμφωνα με το παρακάτω
Λήμμα , ισχύει

όπου

.
Από

στο τρίγωνο

, έχουμε

Από

και


Στο τρίγωνο

τώρα, με διατέμνουσα την

, σύμφωνα με το
Θεώρημα Μενελάου , έχουμε

Από


και το ισοδύναμο ζητούμενο έχει αποδειχθεί.
ΛΗΜΜΑ. - Δίνεται τρίγωνο  και έστω
και έστω  τα ύψη του και ας είναι
τα ύψη του και ας είναι  , τα μέσα των
, τα μέσα των  , αντιστοίχως. Έστω
, αντιστοίχως. Έστω  , οι προβολές του
, οι προβολές του  επί των
επί των  αντιστοίχως και ας είναι
αντιστοίχως και ας είναι  , το σημείο ώστε το
, το σημείο ώστε το  να είναι παραλληλόγραμμο. Αποδείξτε ότι
να είναι παραλληλόγραμμο. Αποδείξτε ότι 
.
Κώστας Βήττας.
ΥΓ. Θα βάλω αργότερα την απόδειξη που έχω υπόψη μου για το ως άνω
Λήμμα.
 και ας είναι
και ας είναι  το συμμετρικό του μέσου
το συμμετρικό του μέσου  της
της  ως προς την
ως προς την  , με
, με  τις ορθές προβολές των
τις ορθές προβολές των  στις
στις  αντίστοιχα και έστω
αντίστοιχα και έστω  . Αν
. Αν  οι ορθές προβολές του
οι ορθές προβολές του  στις
στις  αντίστοιχα , να δειχθεί ότι η τέταρτη κορυφή (έστω
αντίστοιχα , να δειχθεί ότι η τέταρτη κορυφή (έστω  ) του παραλληλογράμμου
) του παραλληλογράμμου  είναι σημείο της ευθείας
είναι σημείο της ευθείας  όπου
όπου  το μέσο της
το μέσο της 
 και ας είναι
και ας είναι  το συμμετρικό του μέσου
το συμμετρικό του μέσου  της
της  ως προς την
ως προς την  , με
, με  τις ορθές προβολές των
τις ορθές προβολές των  στις
στις  αντίστοιχα και έστω
αντίστοιχα και έστω  . Αν
. Αν  οι ορθές προβολές του
οι ορθές προβολές του  στις
στις  αντίστοιχα , να δειχθεί ότι η τέταρτη κορυφή (έστω
αντίστοιχα , να δειχθεί ότι η τέταρτη κορυφή (έστω  ) του παραλληλογράμμου
) του παραλληλογράμμου  είναι σημείο της ευθείας
είναι σημείο της ευθείας  όπου
όπου  το μέσο της
το μέσο της 
 Έστω
Έστω  , τα ύψη του δοσμένου τριγώνου
, τα ύψη του δοσμένου τριγώνου  και ας είναι
και ας είναι  , τα μέσα των
, τα μέσα των  , αντιστοίχως.
, αντιστοίχως. , τα μέσα των
, τα μέσα των  αντιστοίχως και από τα εγγράψιμα τετράπλευρα
αντιστοίχως και από τα εγγράψιμα τετράπλευρα  έχουμε αντιστοίχως,
έχουμε αντιστοίχως,  και
και 
 , προκύπτει ότι τα σημεία
, προκύπτει ότι τα σημεία  είναι συνευθειακά και ας είναι
είναι συνευθειακά και ας είναι  προς το μέρος του
προς το μέρος του  , ώστε να είναι
, ώστε να είναι 
 , οι προβολές του σημείου
, οι προβολές του σημείου  αντιστοίχως και ας είναι
αντιστοίχως και ας είναι  να είναι παραλλήλόγραμμο.
να είναι παραλλήλόγραμμο. , όπου
, όπου  .
.
 , οι προβολές του
, οι προβολές του  αντιστοίχως και ας είναι
αντιστοίχως και ας είναι  , το σημείο ώστε το
, το σημείο ώστε το  να είναι παραλληλόγραμμο.
να είναι παραλληλόγραμμο. , σύμφωνα με το
, σύμφωνα με το 
 οι προβολές τριών συνευθειακών σημείων, επί δύο τεμνόμενων ευθειών, ορίζουν τμήματα με ίσους λόγους
οι προβολές τριών συνευθειακών σημείων, επί δύο τεμνόμενων ευθειών, ορίζουν τμήματα με ίσους λόγους 
 και
και  τώρα, σύμφωνα με το ίδιο θεώρημα ( γενίκευση ), προκύπτει ότι τα σημεία
τώρα, σύμφωνα με το ίδιο θεώρημα ( γενίκευση ), προκύπτει ότι τα σημεία  είναι συνευθειακά.
είναι συνευθειακά. όπου
όπου  .
. στο τρίγωνο
στο τρίγωνο  , έχουμε
, έχουμε 
 και
και 

 τώρα, με διατέμνουσα την
τώρα, με διατέμνουσα την  , σύμφωνα με το
, σύμφωνα με το 

 και το ισοδύναμο ζητούμενο έχει αποδειχθεί.
και το ισοδύναμο ζητούμενο έχει αποδειχθεί. τα ύψη του και ας είναι
τα ύψη του και ας είναι  , τα μέσα των
, τα μέσα των  , αντιστοίχως. Έστω
, αντιστοίχως. Έστω 
 αλληλοδιχοτομούνται και άρα έχουμε
αλληλοδιχοτομούνται και άρα έχουμε  όπου
όπου  .
. , η διαγώνιά του
, η διαγώνιά του  περνάει από το μέσον
περνάει από το μέσον  της
της  και ισχύει
και ισχύει