Όμορφο πρόβλημα. Ότι πρέπει για ένα ΑΛΤΣΟΤΕΣΤ για τους ηλικιωμένους ( > 65 ).


Αλλάζω λίγο τους συμβολισμούς, για ( δική μου ) ευκολία.
Έστω

τα ύψη του δοσμένου τριγώνου

και ας είναι

τα μέσα των πλευρών του

, αντιστοίχως και έστω

τα σημεία στον περίκυκλο

του

, ώστε να είναι

.
Οι δια του κέντρου

του
Κύκλου Euler του

κάθετες ευθείες επί των

, τέμνουν τις

στα σημεία
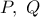
, αντιστοίχως.

Έστω

, τα μέσα των

αντιστοίχως, όπου

είναι το ορθόκεντρο του

και από τα ορθογώνια τρίγωνα

, έχουμε ότι τα

ταυτίζονται με τα αντιδιαμετρικά σημεία των
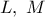
αντιστοίχως, στον
Κύκλο Euler 
του

.
θεωρούμε το εγγεγραμμένο στον κύκλο

, μη κυρτό εξάγωνο

και σύμφωνα με το
Θεώρημα Pascal , έχουμε ότι τα σημεία

και

και

είναι συνευθειακά.

- Όμορφη ομοκυκλικότητα.
- f=185_t=57171.png (40.36 KiB) Προβλήθηκε 1131 φορές

Σύμφωνα με το παρακάτω
Λήμμα , έχουμε ότι

και ομοίως

Από

και

και

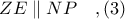
και

Από

και συνευθειακά

τώρα, προκύπτει

Από


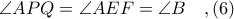
Από

συμπεραίνεται ότι τα σημεία

είναι ομοκυκλικά και το ζητούμενο έχει αποδειχθεί.
ΛΗΜΜΑ. - Δίνεται τρίγωνο  , εγγεγραμμένο σε κύκλο
, εγγεγραμμένο σε κύκλο  και έστω
και έστω  τα ύψη του και
τα ύψη του και  το ορθόκεντρό του. Έστω
το ορθόκεντρό του. Έστω  , το σημείο επί τού τόξου
, το σημείο επί τού τόξου 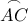 που δεν περιέχει το σημείο
που δεν περιέχει το σημείο  , ώστε να είναι
, ώστε να είναι  . Αποδείξτε ότι
. Αποδείξτε ότι  , όπου
, όπου  είναι το μέσον του
είναι το μέσον του 
.
Κώστας Βήττας.
ΥΓ. Θα βάλω αργότερα την ( απλή ) απόδειξη που έχω υπόψη μου για το ως άνω
Λήμμα.
 είναι τρία ίσα διαδοχικά τόξα κύκλου
είναι τρία ίσα διαδοχικά τόξα κύκλου  με μέτρο μικρότερο των
με μέτρο μικρότερο των  και
και  τυχόν σημείο του υπόλοιπου από τον κύκλο τόξου
τυχόν σημείο του υπόλοιπου από τον κύκλο τόξου  . Να δειχθεί ότι
. Να δειχθεί ότι  είναι ομοκυκλικά , με
είναι ομοκυκλικά , με  τα σημεία τομής των εκ του
τα σημεία τομής των εκ του  καθέτων στις
καθέτων στις  με τις πλευρές
με τις πλευρές  του τριγώνου
του τριγώνου  , όπου
, όπου  είναι το κέντρο του κύκλου Euler του τριγώνου
είναι το κέντρο του κύκλου Euler του τριγώνου 

 Αλλάζω λίγο τους συμβολισμούς, για ( δική μου ) ευκολία.
Αλλάζω λίγο τους συμβολισμούς, για ( δική μου ) ευκολία. τα ύψη του δοσμένου τριγώνου
τα ύψη του δοσμένου τριγώνου  τα μέσα των πλευρών του
τα μέσα των πλευρών του  , αντιστοίχως και έστω
, αντιστοίχως και έστω  τα σημεία στον περίκυκλο
τα σημεία στον περίκυκλο  του
του  .
. , τέμνουν τις
, τέμνουν τις  στα σημεία
στα σημεία 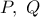 , αντιστοίχως.
, αντιστοίχως.  , τα μέσα των
, τα μέσα των  αντιστοίχως, όπου
αντιστοίχως, όπου  είναι το ορθόκεντρο του
είναι το ορθόκεντρο του  , έχουμε ότι τα
, έχουμε ότι τα 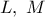 αντιστοίχως, στον
αντιστοίχως, στον  του
του  και σύμφωνα με το
και σύμφωνα με το  και
και  και
και  είναι συνευθειακά.
είναι συνευθειακά.
 και ομοίως
και ομοίως 
 και
και  και
και 
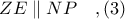 και
και 
 και συνευθειακά
και συνευθειακά  τώρα, προκύπτει
τώρα, προκύπτει 


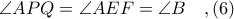
 συμπεραίνεται ότι τα σημεία
συμπεραίνεται ότι τα σημεία  είναι ομοκυκλικά και το ζητούμενο έχει αποδειχθεί.
είναι ομοκυκλικά και το ζητούμενο έχει αποδειχθεί. τα ύψη του και
τα ύψη του και  , το σημείο επί τού τόξου
, το σημείο επί τού τόξου 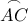 που δεν περιέχει το σημείο
που δεν περιέχει το σημείο  , ώστε να είναι
, ώστε να είναι  . Αποδείξτε ότι
. Αποδείξτε ότι  , όπου
, όπου  είναι το μέσον του
είναι το μέσον του 
 και ας είναι
και ας είναι  , η προβολή του
, η προβολή του  .
.
 λόγω του ορθογωνίου τριγώνου
λόγω του ορθογωνίου τριγώνου  με
με  .
. και το ισοσκελές τρίγωνο
και το ισοσκελές τρίγωνο 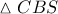 με
με  προκύπτει
προκύπτει 
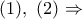

 συμπεραίνεται ότι το τετράπλευρο
συμπεραίνεται ότι το τετράπλευρο  είναι εγγράψιμο και επομένως ισχύει
είναι εγγράψιμο και επομένως ισχύει  και το
και το 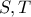 οι ορθές προβολές του
οι ορθές προβολές του  και ας είναι
και ας είναι  τα σημεία τομής των εκ των
τα σημεία τομής των εκ των 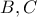 καθέτων στις
καθέτων στις  με τις
με τις  αντίστοιχα.
αντίστοιχα. οπότε σύμφωνα με το
οπότε σύμφωνα με το .
.
