Τη μοιράζομαι μαζί σας, με την ελπίδα να μην έχει συζητηθεί πιο παλιά στο forum...
Σε τρίγωνο
 ισχύει ότι
ισχύει ότι 
Συντονιστές: vittasko, silouan, Doloros
 ισχύει ότι
ισχύει ότι 
Καλησπέρα κ. ΤηλέμαχεΚΕΦΑΛΟΝΙΤΗΣ έγραψε: ↑Παρ Ιουν 24, 2022 3:48 pmΣήμερα το πρωί στο γραφείο των καθηγητών, ανάμεσα σε βαθμούς απολυτηρίων και μητρώα, βρήκα λίγο χρόνο να δω μια ανισότητα...
Τη μοιράζομαι μαζί σας, με την ελπίδα να μην έχει συζητηθεί πιο παλιά στο forum...
Σε τρίγωνοισχύει ότι

 , οπότε κάνοντας την αντικατάσταση Ravi (
, οπότε κάνοντας την αντικατάσταση Ravi ( ), είναι
), είναι , άρα
, άρα  .
.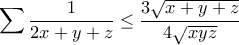
 , και άρα αρκεί να δείξουμε ότι
, και άρα αρκεί να δείξουμε ότι

 , που ισχύει καθώς
, που ισχύει καθώς  όπου η προτελευταία ανισότητα ισχύει διότι
όπου η προτελευταία ανισότητα ισχύει διότι  .
.
 δεν είναι ουρανοκατέβατη. Χρησιμοποιούμε την Tangent Line method.
δεν είναι ουρανοκατέβατη. Χρησιμοποιούμε την Tangent Line method.Καλημέρα σε όλους!ΚΕΦΑΛΟΝΙΤΗΣ έγραψε: ↑Παρ Ιουν 24, 2022 3:48 pmΣήμερα το πρωί στο γραφείο των καθηγητών, ανάμεσα σε βαθμούς απολυτηρίων και μητρώα, βρήκα λίγο χρόνο να δω μια ανισότητα...
Τη μοιράζομαι μαζί σας, με την ελπίδα να μην έχει συζητηθεί πιο παλιά στο forum...
Σε τρίγωνοισχύει ότι

 η περίμετρος,
η περίμετρος,  η ακτίνα του περιγεγραμμένου κύκλου και
η ακτίνα του περιγεγραμμένου κύκλου και  το εμβαδόν του τριγώνου. Ως γνωστόν είναι:
το εμβαδόν του τριγώνου. Ως γνωστόν είναι:






 Πράγματι,
Πράγματι, 
 όπου με πρόσθεση κατά μέλη και από την
όπου με πρόσθεση κατά μέλη και από την 
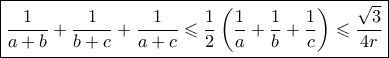

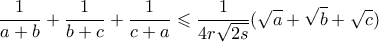

 τέτοιο ώστε
τέτοιο ώστε 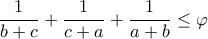

 αποτελούν πλευρές τριγώνου.
αποτελούν πλευρές τριγώνου. το εμβαδόν και η ημιπερίμετρος αντίστοιχα του τριγώνου με πλευρές
το εμβαδόν και η ημιπερίμετρος αντίστοιχα του τριγώνου με πλευρές 





 η ακτίνα του εγγεγραμμένου κύκλου του τριγώνου με πλευρές
η ακτίνα του εγγεγραμμένου κύκλου του τριγώνου με πλευρές 

 ισχύει ότι
ισχύει ότι  από τη δημοσίευση
από τη δημοσίευση η ανισότητα αυτή γράφεται
η ανισότητα αυτή γράφεται

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες