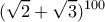 προκύπτει ένα άθροισμα με 101 προσθετέους. Ποιος είναι ο μεγαλύτερος από αυτούς;
προκύπτει ένα άθροισμα με 101 προσθετέους. Ποιος είναι ο μεγαλύτερος από αυτούς;Μέγιστος όρος αναπτύγματος!
Συντονιστές: achilleas, emouroukos, silouan
- matha
- Γενικός Συντονιστής
- Δημοσιεύσεις: 6423
- Εγγραφή: Παρ Μάιος 21, 2010 7:40 pm
- Τοποθεσία: Θεσσαλονίκη
Μέγιστος όρος αναπτύγματος!
Αναπτύσσοντας το 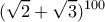 προκύπτει ένα άθροισμα με 101 προσθετέους. Ποιος είναι ο μεγαλύτερος από αυτούς;
προκύπτει ένα άθροισμα με 101 προσθετέους. Ποιος είναι ο μεγαλύτερος από αυτούς;
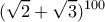 προκύπτει ένα άθροισμα με 101 προσθετέους. Ποιος είναι ο μεγαλύτερος από αυτούς;
προκύπτει ένα άθροισμα με 101 προσθετέους. Ποιος είναι ο μεγαλύτερος από αυτούς;Μάγκος Θάνος
Λέξεις Κλειδιά:
-
Manolis Petrakis
- Δημοσιεύσεις: 204
- Εγγραφή: Τετ Οκτ 07, 2020 3:19 pm
- Τοποθεσία: Αγρίνιο
Re: Μέγιστος όρος αναπτύγματος!
Χαίρεται!

Κάθε προσθετέος είναι της μορφής
Για είναι
είναι 


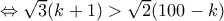


Ομοίως είναι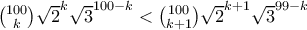
Για
Από τις 2 αυτές σχέσεις παίρνουμε:

Και:
Από τις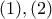 παίρνουμε ότι ο
παίρνουμε ότι ο 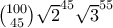 είναι ο μεγαλύτερος προσθετέος
είναι ο μεγαλύτερος προσθετέος

Κάθε προσθετέος είναι της μορφής

Για
 είναι
είναι 


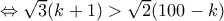


Ομοίως είναι
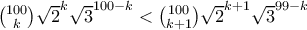
Για

Από τις 2 αυτές σχέσεις παίρνουμε:

Και:

Από τις
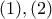 παίρνουμε ότι ο
παίρνουμε ότι ο 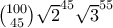 είναι ο μεγαλύτερος προσθετέος
είναι ο μεγαλύτερος προσθετέοςRe: Μέγιστος όρος αναπτύγματος!
Ο νιοστός όρος του αναπτύγματος είναι  και ο ν+1-οστός είναι
και ο ν+1-οστός είναι  άρα αρκεί να λύσω
άρα αρκεί να λύσω  και προκύπτει
και προκύπτει  όμως αφού
όμως αφού 
 άρα επόμενος όρος δηλαδή ο
άρα επόμενος όρος δηλαδή ο 
είναι ο μεγαλύτερος.
 και ο ν+1-οστός είναι
και ο ν+1-οστός είναι  άρα αρκεί να λύσω
άρα αρκεί να λύσω  και προκύπτει
και προκύπτει  όμως αφού
όμως αφού 
 άρα επόμενος όρος δηλαδή ο
άρα επόμενος όρος δηλαδή ο 
είναι ο μεγαλύτερος.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες
