 .
.Για κάθε
![x\in[-1,1] x\in[-1,1]](/forum/ext/geomar/texintegr/latexrender/pictures/3fc4488933571bb861da5bf45c51cbc8.png) ισχύει:
ισχύει: 
Δείξτε ότι για κάθε
![x\in[-1,1] x\in[-1,1]](/forum/ext/geomar/texintegr/latexrender/pictures/3fc4488933571bb861da5bf45c51cbc8.png) ισχύει:
ισχύει: 
Συντονιστές: achilleas, emouroukos, silouan
 .
.![x\in[-1,1] x\in[-1,1]](/forum/ext/geomar/texintegr/latexrender/pictures/3fc4488933571bb861da5bf45c51cbc8.png) ισχύει:
ισχύει: 
![x\in[-1,1] x\in[-1,1]](/forum/ext/geomar/texintegr/latexrender/pictures/3fc4488933571bb861da5bf45c51cbc8.png) ισχύει:
ισχύει: 
Θα γραψω σύντομη απάντηση.Λάμπρος Κατσάπας έγραψε: ↑Τετ Ιούλ 22, 2020 10:12 amΔίνονται.
Για κάθεισχύει:
Δείξτε ότι για κάθεισχύει:

 (γιατί ; )
(γιατί ; ) και
και 





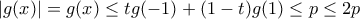

 (1)
(1) είναι
είναι 

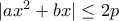
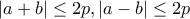 (2)
(2)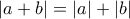 η
η 

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες