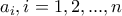


όπου

Αν

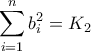

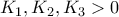
να βρεθεί η μέγιστη τιμή της παράστασης

Συντονιστές: achilleas, emouroukos, silouan
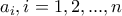




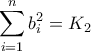

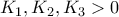

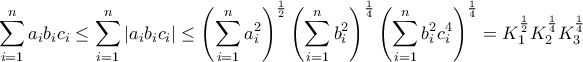
 για θετικές σταθερές
για θετικές σταθερές  . Ενδεικτικά έχουμε ισότητα, όταν όλα τα
. Ενδεικτικά έχουμε ισότητα, όταν όλα τα  είναι ίσα, τα
είναι ίσα, τα 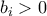 είναι ίσα, τα
είναι ίσα, τα 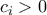 είναι ίσα.
είναι ίσα.AM-GMΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τρί Ιουν 30, 2020 6:43 pmΘεωρούμε τους πραγματικούς
όπου
Αν
να βρεθεί η μέγιστη τιμή της παράστασης

![2a_i^2+b_i^2+b_i^2c_i^4\geq 4 \sqrt [4]{a_i^4b_i^4c_i^4}=4|a_ib_ic_i|\geq 4a_ib_ic_i 2a_i^2+b_i^2+b_i^2c_i^4\geq 4 \sqrt [4]{a_i^4b_i^4c_i^4}=4|a_ib_ic_i|\geq 4a_ib_ic_i](/forum/ext/geomar/texintegr/latexrender/pictures/a533e8eef49acf3c16d173c7014d7d19.png)
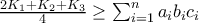
 , με
, με 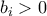 .
.Το μέγιστο ποιο είναι;miltosk έγραψε: ↑Τρί Ιουν 30, 2020 8:00 pmAM-GMΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τρί Ιουν 30, 2020 6:43 pmΘεωρούμε τους πραγματικούς
όπου
Αν
να βρεθεί η μέγιστη τιμή της παράστασης

Αθροίζοντας:
Η ισότητα στην τελευταία για, με
.
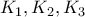 είναι οποιαδήποτε .
είναι οποιαδήποτε .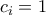 τότε
τότε 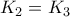
ΤοΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τρί Ιουν 30, 2020 8:23 pmΤο μέγιστο ποιο είναι;miltosk έγραψε: ↑Τρί Ιουν 30, 2020 8:00 pmAM-GMΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τρί Ιουν 30, 2020 6:43 pmΘεωρούμε τους πραγματικούς
όπου
Αν
να βρεθεί η μέγιστη τιμή της παράστασης

Αθροίζοντας:
Η ισότητα στην τελευταία για, με
.
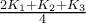 . Τα
. Τα  δεν θεωρούνται μεταβλητά και τα
δεν θεωρούνται μεταβλητά και τα  σταθερά;
σταθερά;Οχι δεν ταυτίζονται .miltosk έγραψε: ↑Τρί Ιουν 30, 2020 8:30 pmΤοΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τρί Ιουν 30, 2020 8:23 pmΤο μέγιστο ποιο είναι;miltosk έγραψε: ↑Τρί Ιουν 30, 2020 8:00 pmAM-GMΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τρί Ιουν 30, 2020 6:43 pmΘεωρούμε τους πραγματικούς
όπου
Αν
να βρεθεί η μέγιστη τιμή της παράστασης

Αθροίζοντας:
Η ισότητα στην τελευταία για, με
.
. Τα
δεν θεωρούνται μεταβλητά και τα
σταθερά;
Νομίζω στην περίπτωση ισότητας, ταυτίζεται με αυτό που δίνει ο giannisd πιο πάνω.
 είναι ίσα ,όλα τα
είναι ίσα ,όλα τα  είναι ίσα και όλα τα
είναι ίσα και όλα τα 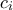 είναι ίσα.
είναι ίσα.Τίποτα δεν χάνεις.
 μη αρνητικά.
μη αρνητικά.
 (1)
(1)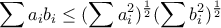 (2)
(2) (3)
(3)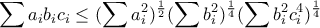
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 19 επισκέπτες