Ανισότητα με διατεταγμένους αριθμούς

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ · #1

Θεωρούμε τούς
$\displaystyle 1\geq a_{1}\geq a_{2}\geq ....\geq a_{n}\geq 0,n\geq 2$
Να δειχθεί ότι
$\displaystyle (1-a_{1})(1-a_{2})...(1-a_{n})+a_{1}\geq \frac{1}{(1+a_{2})(1+a_{3})...(1+a_{n})}$

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ · #2

Επαναφορά.
Η ανισότητα είναι για να αποδειχθεί μια άλλη.
Αυτή βρίσκεται στο
viewtopic.php?f=59&t=15824

Λάμπρος Κατσάπας · #3

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑
Πέμ Δεκ 19, 2019 8:22 pm
Θεωρούμε τούς
$\displaystyle 1\geq a_{1}\geq a_{2}\geq ....\geq a_{n}\geq 0,n\geq 2$
Να δειχθεί ότι
$\displaystyle (1-a_{1})(1-a_{2})...(1-a_{n})+a_{1}\geq \frac{1}{(1+a_{2})(1+a_{3})...(1+a_{n})}$

Μπορεί να συμμαζεύεται η παρακάτω αλλά λόγω ώρας αδυνατώ να το κοιτάξω.

Για να τη φέρουμε σε μια πιο ευανάγνωστη μορφή θέτουμε $b_i=\dfrac{1}{1+a_i}$ για i=2,3,...,n

,

καθώς και

για

.

Θέλουμε να δείξουμε ότι $b_1-c_1\geq \prod_{i=1}^{n}b_i-\prod_{i=1}^{n}c_i.$

Γράφουμε τώρα

$\dislaystyle\prod_{i=1}^{n}b_i-\prod_{i=1}^{n}c_i =(b_1-c_1)c_2c_3...c_n+b_1(b_2-c_2)c_3...c_n+...+b_1b_2...b_{n-1}(b_n-c_n)$

Προχωράμε με επαγωγή.

Για n=2

έχουμε ότι η $\dislaystyle(b_1-c_1)c_2+b_1(b_2-c_2)\leq b_ 1-c_1$

είναι ισοδύναμη με την $0\leq a_2(a_1-a_2)+a_1a_{2}^{2}$ που ισχύει.

Υποθέτουμε ότι ισχύει για $n=k\geq 2$ και θα δείξουμε ότι ισχύει για n=k+1.

Είναι

$\dislaystyle\prod_{i=1}^{k+1}b_i-\prod_{i=1}^{k+1}c_i =$

$\dislaystyle(b_1-c_1)c_2c_3...c_{k+1}+b_1(b_2-c_2)c_3...c_{k+1}+...+b_1b_2...b_{k-1}(b_k-c_k)c_{k+1}+b_1b_2...b_k(b_{k+1}-c_{k+1})$

$\dislaystyle\leq (b_1-c_1)c_{k+1}+b_1b_2...b_k(b_{k+1}-c_{k+1}).$

H $(b_1-c_1)c_{k+1}+b_1b_2...b_k(b_{k+1}-c_{k+1})\leq b_1-c_1$ είναι ισοδύναμη με την

$\dfrac{1}{1+a_2}\dfrac{1}{1+a_3}...\dfrac{1}{1+a_k}\dfrac{a_{k+1}^{2}}{1+a_{k+1}}\leq a_1a_{k+1}$

που με τη σειρά της είναι ισοδύναμη με την $a_{k+1}\leq a_1 \left ( 1+a_2 \right )\left ( 1+a_3 \right )...\left ( 1+a_{k+1} \right )$

που ισχύει, αφού $a_{k+1}\leq a_1\leq a_1 \left ( 1+a_2 \right )\left ( 1+a_3 \right )...\left ( 1+a_{k+1} \right ).$

#4

Πολλαπλασιάζοντας τα δύο σκέλη της ανισότητας με τον παρονομαστή του δεξιού σκέλους και κρατώντας μόνον τους αρνητικούς όρους του αριστερού σκέλους καταλήγουμε σε μία ανισότητα που προκύπτει άμεσα από τους όρους του προβλήματος (και κάτι λιγότερο, αρκεί να έχουμε $0\leq a_1\leq 1$ και να είναι ο a_1

μεγαλύτερος ή ίσος των υπολοίπων). Γράφω τις σχετικές ανισότητες για n=2

,

(παραλείποντας τον γενικό τύπο):

$a_2^2\leq a_1a_2$

$(a_2^2+a_3^2)+a_1(a_2^2a_3^2)\leq a_1(a_2+a_3)+a_1(a_2a_3)$

$(a_2^2+a_3^2+a_4^2)+a_1(a_2^2a_3^2+a_2^2a_4^2+a_3^2a_4^2)\leq a_1(a_2+a_3+a_4)+a_1(a_2a_3+a_2a_4+a_3a_4)$

#5

gbaloglou έγραψε: ↑
Δευ Δεκ 23, 2019 1:48 am
Πολλαπλασιάζοντας τα δύο σκέλη της ανισότητας με τον παρονομαστή του δεξιού σκέλους και κρατώντας μόνον τους αρνητικούς όρους του αριστερού σκέλους καταλήγουμε σε μία ανισότητα που προκύπτει άμεσα από τους όρους του προβλήματος (και κάτι λιγότερο, αρκεί να έχουμε $0\leq a_1\leq 1$ και να είναι ο μεγαλύτερος ή ίσος των υπολοίπων). Γράφω τις σχετικές ανισότητες για , , (παραλείποντας τον γενικό τύπο):

$a_2^2\leq a_1a_2$

$(a_2^2+a_3^2)+a_1(a_2^2a_3^2)\leq a_1(a_2+a_3)+a_1(a_2a_3)$

$(a_2^2+a_3^2+a_4^2)+a_1(a_2^2a_3^2+a_2^2a_4^2+a_3^2a_4^2)\leq a_1(a_2+a_3+a_4)+a_1(a_2a_3+a_2a_4+a_3a_4)$

Ιδού και ο 'γενικός τύπος' (που δεν παρέθεσα χθες βράδυ λόγω έλλειψης χρόνου), η ανισότητα που ξεκλειδώνει το πρόβλημα:

$a_1+\sum_{2\leq i_i\leq n}a_i_1^2+a_1\sum_{2\leq i_i<i_2\leq n}a_i_1^2a_i_2^2+\sum_{2\leq i_i<i_2<i_3\leq n}a_i_1^2a_i_2^2a_i_3^2+a_1\sum_{2\leq i_i<i_2<i_3<i_4\leq n}a_i_1^2a_i_2^2a_i_3^2a_i_4^2+$

$\leq$

$a_1+a_1\sum_{2\leq i_i\leq n}a_i_1+a_1\sum_{2\leq i_i<i_2\leq n}a_i_1a_i_2+a_1\sum_{2\leq i_i<i_2<i_3\leq n}a_i_1a_i_2a_i_3+a_1\sum_{2\leq i_i<i_2<i_3<i_4\leq n}a_i_1a_i_2a_i_3a_i_4+$

#6

Έστω $x \in [0,1]$ . Ορίζουμε $\displaystyle f(a_2,\ldots,a_n) = (1-x)(1-a_2)\cdots (1-a_n) + x - \frac{1}{(1+a_2) \cdots (1+a_n)}$ για $a_2,\ldots,a_n \in [0,x]$ . (Δεν θέτω περιορισμό διάταξης στα $a_2,\ldots,a_n$ )

Η

είναι κοίλη σε κάθε μεταβλητή a_k

( $k \geqslant 2$ ) οπότε η

παίρνει ελάχιστη τιμή στα άκρα. Επομένως όταν η

ελαχιστοποιείται τα a_i

είναι ίσα με

ή

. H ελάχιστη τιμή της

ισούται με

$\displaystyle a_k = (1-x)^{k+1} + x - \frac{1}{(1+x)^k}$

για κάποιο $k \in \{0,1,\ldots,n-1\}$ . Ισχύει όμως ότι $0 = a_0 \leqslant a_1 \leqslant a_2 \leqslant \cdots$ αφού

$\begin{aligned} a_{k+1} - a_k &= \left[(1-x)^{k+2} - (1-x)^{k+1}\right] - \left[\frac{1}{(1+x)^{k+1}}-\frac{1}{(1+x)^k} \right] \\ &= -x(1-x)^{k+1} + \frac{x}{(1+x)^{k+1}} \\ &= \frac{x}{(1-x)^{k+1}}\left[1-(1-x^2)^{k+1}\right]\geqslant 0. \end{aligned}$

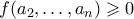Άρα $f(a_2,\ldots,a_n) \geqslant 0$ για κάθε $a_2,\ldots,a_n \in [0,x]$ και επομένως η αρχική ανισότητα είναι αληθής.

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ · #7

Η ανισότητα γράφεται
$\displaystyle a_{1}\geq \frac{1}{(1+a_{2})(1+a_{3})...(1+a_{n})}-(1-a_{1})(1-a_{2})...(1-a_{n})$

επαγωγή στο

Για

απλές πράξεις.
Στο επαγωγικό βήμα αρκει να δειχθεί ότι
$\displaystyle \frac{1}{(1+a_{2})(1+a_{3})...(1+a_{n})}-(1-a_{1})(1-a_{2})...(1-a_{n})\geq$
$\displaystyle\frac{1}{(1+a_{2})(1+a_{3})...(1+a_{n})(1+a_{n+1})}-(1-a_{1})(1-a_{2})...(1-a_{n})(1-a_{n+1})$
η

$\displaystyle\frac{a_{n+1}}{(1+a_{2})(1+a_{3})...(1+a_{n})(1+a_{n+1})}\geq (1-a_{1})(1-a_{2})...(1-a_{n})a_{n+1}$
η

$\displaystyle 1\geq (1-a_{1})(1+a_{n+1})(1-a_{2}^{2})...(1-a_{n}^{2})$

που τετριμμένα ισχύει αφού
$\displaystyle (1-a_{1})(1+a_{n+1})\leq (1-a_{1})(1+a_{1})=1-a_{1}^{2}\leq 1$

Προφανώς η διάταξη δεν χρειάζεται παρά μόνο το μεγαλύτερο.
Το έβαλα έτσι γιατί έτσι τα είχε βάλει ο Πέτρος στην αρχική ανισότητα που δημιούργησε αυτήν.

Ανισότητα με διατεταγμένους αριθμούς

Ανισότητα με διατεταγμένους αριθμούς

Re: Ανισότητα με διατεταγμένους αριθμούς

Re: Ανισότητα με διατεταγμένους αριθμούς

Re: Ανισότητα με διατεταγμένους αριθμούς

Re: Ανισότητα με διατεταγμένους αριθμούς

Re: Ανισότητα με διατεταγμένους αριθμούς

Re: Ανισότητα με διατεταγμένους αριθμούς

Μέλη σε σύνδεση