![P\left( x \right), Q\left( x \right) \in \mathbb{R}\left[ x \right] P\left( x \right), Q\left( x \right) \in \mathbb{R}\left[ x \right]](/forum/ext/geomar/texintegr/latexrender/pictures/d663c22c2737aa17d112bee80c78c001.png) δύο πολυώνυμα τέτοια, ώστε να ισχύει
δύο πολυώνυμα τέτοια, ώστε να ισχύει 
Να αποδείξετε ότι υπάρχει πολυώνυμο
![R\left( x \right) \in \mathbb{R}\left[ x \right] R\left( x \right) \in \mathbb{R}\left[ x \right]](/forum/ext/geomar/texintegr/latexrender/pictures/9f07fceb5610cb0f0bbb18eda543ac34.png) τέτοιο, ώστε
τέτοιο, ώστε 
Συντονιστές: achilleas, emouroukos, silouan
![P\left( x \right), Q\left( x \right) \in \mathbb{R}\left[ x \right] P\left( x \right), Q\left( x \right) \in \mathbb{R}\left[ x \right]](/forum/ext/geomar/texintegr/latexrender/pictures/d663c22c2737aa17d112bee80c78c001.png) δύο πολυώνυμα τέτοια, ώστε να ισχύει
δύο πολυώνυμα τέτοια, ώστε να ισχύει 
![R\left( x \right) \in \mathbb{R}\left[ x \right] R\left( x \right) \in \mathbb{R}\left[ x \right]](/forum/ext/geomar/texintegr/latexrender/pictures/9f07fceb5610cb0f0bbb18eda543ac34.png) τέτοιο, ώστε
τέτοιο, ώστε 
 ,
,

 με
με  τέτοιο ώστε:
τέτοιο ώστε:
 θα είναι ο
θα είναι ο
 είναι ο
είναι ο 
 πρέπει οι μεγιστοβαθμιοι όροι τος να είναι ίσοι
πρέπει οι μεγιστοβαθμιοι όροι τος να είναι ίσοι  (1)και
(1)και 
 άρτιος ,
άρτιος ,  περιττός
περιττός  να είναι τετράγωνο πραγματικού(έστω
να είναι τετράγωνο πραγματικού(έστω 
 ισχύει ότι
ισχύει ότι  και πολυωνυμα της μορφής
και πολυωνυμα της μορφής 
 (2)
(2) είναι και ριζες του
είναι και ριζες του 


 (3)
(3)

 ,άτοπο
,άτοπο 


Ο συλλογισμόςchristinat έγραψε: ↑Κυρ Ιαν 12, 2020 11:43 pmΈστω,
Τοτε
Έστω ακόμη πολυωνυμομε
τέτοιο ώστε:
Ο μεγιστοβαθμιος όρος τουθα είναι ο
Ενώ ο μεγιστοβαθμιος όρος τουείναι ο
Αφούπρέπει οι μεγιστοβαθμιοι όροι τος να είναι ίσοι
Οποτε(1)και
άρτιος ,
περιττός
Λόγω της (1) πρέπεινα είναι τετράγωνο πραγματικού(έστω
Έστω τωρα ότι για κάποιοισχύει ότι
και πολυωνυμα της μορφής
(2)
Οι ριζες των πολυωνυμων της μορφήςείναι και ριζες του
άρα και του
(3)
Από τις εχεις (2)-(3) προκύπτει ότι:
,άτοπο
Άρα
Υπάρχει λοιπόν πολυωνυμο
 είναι και ριζες του
είναι και ριζες του 




 ώστε να ισχύει η
ώστε να ισχύει η 

Γράφω λύση.emouroukos έγραψε: ↑Σάβ Οκτ 05, 2019 12:34 pmΈστωδύο πολυώνυμα τέτοια, ώστε να ισχύει
Να αποδείξετε ότι υπάρχει πολυώνυμοτέτοιο, ώστε

 (1)
(1) είναι ο βαθμός του
είναι ο βαθμός του  και
και  του
του  ,τότε
,τότε
 είναι άρτιος.
είναι άρτιος. έχουν άρτιο βαθμό πολλαπλότητας οπότε
έχουν άρτιο βαθμό πολλαπλότητας οπότε  ρίζα του
ρίζα του  με πολλαπλότητα
με πολλαπλότητα  περιττό.
περιττό.


 εχουν όλες πολλαπλότητα άρτιο
εχουν όλες πολλαπλότητα άρτιο  (2)
(2) είναι άρτιος θα υπάρχει και άλλη ρίζα του
είναι άρτιος θα υπάρχει και άλλη ρίζα του  έστω
έστω 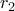
 περιττό.
περιττό. (3).
(3). (4)
(4)

 έχουν άρτιο βαθμό πολλαπλότητας.
έχουν άρτιο βαθμό πολλαπλότητας.![\mathbb{R}[x ] \mathbb{R}[x ]](/forum/ext/geomar/texintegr/latexrender/pictures/7aa44acefceb19e3af9cb6c6016baec6.png) η στο
η στο ![\mathbb{C}[x] \mathbb{C}[x]](/forum/ext/geomar/texintegr/latexrender/pictures/7691ae2741fe5511ac2228c38a45ab50.png) .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες