 για τους οποίους η παρακάτω παράσταση πέρνει την ελάχιστη τιμή της
για τους οποίους η παρακάτω παράσταση πέρνει την ελάχιστη τιμή της
πηγή Aops
Συντονιστές: achilleas, emouroukos, silouan
 για τους οποίους η παρακάτω παράσταση πέρνει την ελάχιστη τιμή της
για τους οποίους η παρακάτω παράσταση πέρνει την ελάχιστη τιμή της
Xriiiiistos έγραψε: ↑Σάβ Ιούλ 07, 2018 11:23 pmNα βρεθεί η τιμή των θετικών πραγματικών αριθμώνγια τους οποίους η παρακάτω παράσταση πέρνει την ελάχιστη τιμή της
πηγή Aops

 και
και  τα οποία είναι αντίστροφοι όροι.
τα οποία είναι αντίστροφοι όροι.
 σύμφωνα με τη γνωστή ανισότητα και αφού
σύμφωνα με τη γνωστή ανισότητα και αφού 
 δηλαδή όταν
δηλαδή όταν 
 ,
,  ,
,  βρίσκουμε ότι:
βρίσκουμε ότι:



 από τη δεύτερη και την τρίτη ότι
από τη δεύτερη και την τρίτη ότι 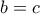 και από τις δύο τελευταίες ότι
και από τις δύο τελευταίες ότι 



 (1), για
(1), για  .
. .
. (2).
(2).
 .
. (3).
(3). , άρα είναι
, άρα είναι  .
. .
.Γεια σου Γιώργο.Γιώργος Ρίζος έγραψε: ↑Κυρ Ιούλ 08, 2018 3:28 pm
Θέτω το ερώτημα: Το παραπάνω θεώρημα ισχύει και αντίστροφα;
Δηλαδή αν το γινόμενο θετικών παραγόντων είναι σταθερό, αλλά οι παράγοντες δεν μπορούν να γίνουν ίσοι, τότε μπορεί το άθροισμά τους να έχει ελάχιστο;
Δείτε σχετική συζήτηση (για παρόμοια περίπτωση) ΕΔΩ.
Η παράσταση είναι ομογενής.Xriiiiistos έγραψε: ↑Σάβ Ιούλ 07, 2018 11:23 pmNα βρεθεί η τιμή των θετικών πραγματικών αριθμώνγια τους οποίους η παρακάτω παράσταση πέρνει την ελάχιστη τιμή της
πηγή Aops




 με περιορισμό
με περιορισμό 



 και
και  είναι γνήσια κυρτές για
είναι γνήσια κυρτές για  ελαχιστοποιούνται οι παραστάσεις
ελαχιστοποιούνται οι παραστάσεις  και
και 

 την
την 
 είναι ίσα.
είναι ίσα. με
με  διάστημα ισχύει
διάστημα ισχύει 



 είναι ίσα.
είναι ίσα.
Καλησπέρα σε όλους. Κάνω μια προσπάθεια με τα εργαλεία που προαναφέραμε, έχοντας εκ των προτέρων "εκτιμήσει" το ελάχιστο, μετά την απάντηση του Σταύρου.Xriiiiistos έγραψε: ↑Σάβ Ιούλ 07, 2018 11:23 pmNα βρεθεί η τιμή των θετικών πραγματικών αριθμώνγια τους οποίους η παρακάτω παράσταση πέρνει την ελάχιστη τιμή της
πηγή Aops




 και το δεύτερο
και το δεύτερο  .
. , σταθερό.
, σταθερό.
 (1)
(1) .
. (2)
(2) (3)
(3) (4)
(4) (5)
(5)


 κι έχουμε το μικρότερο άθροισμα για το
κι έχουμε το μικρότερο άθροισμα για το  , που είναι
, που είναι  .
.  ,
,  , οπότε τότε θα έχουμε και το ελάχιστο άθροισμα
, οπότε τότε θα έχουμε και το ελάχιστο άθροισμα  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης