Πολυώνυμο
Δημοσιεύτηκε: Κυρ Ιουν 10, 2018 6:26 pm
Να βρεθούν όλα τα πολυώνυμα  με πραγματικούς συντελεστές τέτοια ώστε
με πραγματικούς συντελεστές τέτοια ώστε

για κάθε με
με 
 με πραγματικούς συντελεστές τέτοια ώστε
με πραγματικούς συντελεστές τέτοια ώστε 
για κάθε
 με
με 
 με πραγματικούς συντελεστές τέτοια ώστε
με πραγματικούς συντελεστές τέτοια ώστε 
 με
με 
Απάντηση: Τα πολυώνυμα
 .
. , η δοθείσα γίνεται
, η δοθείσα γίνεται  , και άρα ως άνω. Για μη σταθερά είναι
, και άρα ως άνω. Για μη σταθερά είναι  με
με  .
. στη αρχική έχουμε
στη αρχική έχουμε 
 στα δύο μέλη, παίρνουμε
στα δύο μέλη, παίρνουμε 
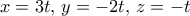 παίρνουμε
παίρνουμε  και άρα
και άρα 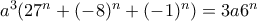
 .
.  . Είναι μοναδική γιατί η προηγούμενη γράφεται
. Είναι μοναδική γιατί η προηγούμενη γράφεται δηλαδή
δηλαδή  ή
ή που εύκολα βλέπουμε ότι δεν μπορεί να ισχύει αν
που εύκολα βλέπουμε ότι δεν μπορεί να ισχύει αν  .
. και πίσω στην
και πίσω στην  παίρνουμε
παίρνουμε  . Και λοιπά.
. Και λοιπά.Εχουμε για

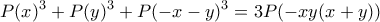
 σταθερό και παραγωγίζοντας ως προς
σταθερό και παραγωγίζοντας ως προς  παίρνουμε
παίρνουμε 
 σταθερό και υποθέτοντας ότι ο βαθμός του πολυωνύμου είναι
σταθερό και υποθέτοντας ότι ο βαθμός του πολυωνύμου είναι 
 βαθμό
βαθμό  .
.  βαθμό
βαθμό  .
. δηλαδή
δηλαδή  .
. .
.