 είναι πλευρές τριγώνου, για τις οποίες ισχύει
είναι πλευρές τριγώνου, για τις οποίες ισχύει  να βρεθεί η ελάχιστη τιμή της παράστασης
να βρεθεί η ελάχιστη τιμή της παράστασης .
.Συντονιστές: achilleas, emouroukos, silouan
 είναι πλευρές τριγώνου, για τις οποίες ισχύει
είναι πλευρές τριγώνου, για τις οποίες ισχύει  να βρεθεί η ελάχιστη τιμή της παράστασης
να βρεθεί η ελάχιστη τιμή της παράστασης .
. είναι πλευρές τριγώνου άρα υπάρχουν θετικοί αριθμοί
είναι πλευρές τριγώνου άρα υπάρχουν θετικοί αριθμοί  ώστε
ώστε  .
.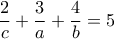 γίνεται
γίνεται 

 (με ισότητα για
(με ισότητα για  ) παίρνουμε:
) παίρνουμε:
 . Η ισότητα ισχύει αν και μόνο αν
. Η ισότητα ισχύει αν και μόνο αν  δηλαδή αν και μόνο αν
δηλαδή αν και μόνο αν  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης