 είναι θετικοί πραγματικοί αριθμοί,έτσι ώστε
είναι θετικοί πραγματικοί αριθμοί,έτσι ώστε  να δείξετε οτι
να δείξετε οτι 
Συντονιστές: achilleas, emouroukos, silouan
 είναι θετικοί πραγματικοί αριθμοί,έτσι ώστε
είναι θετικοί πραγματικοί αριθμοί,έτσι ώστε  να δείξετε οτι
να δείξετε οτι 
Edit: λάθος λύση.Datis-Kalali έγραψε:Ανείναι θετικοί πραγματικοί αριθμοί,έτσι ώστε
να δείξετε οτι
Επειδή μας παρακολουθούν μαθητές που θα συμμετάσχουν σε Διαγωνισμούς επιπέδου Αρχιμήδη και άνω, πρέπει να αναφέρουμε ότι μία τέτοια "λύση" βαθμολογείται με ΜΗΔΕΝ βαθμούς!Friedoon έγραψε:Datis-Kalali έγραψε:Ανείναι θετικοί πραγματικοί αριθμοί,έτσι ώστε
να δείξετε οτι
Άρα από
με
παίρνουμε πως η παράστασημε τον περιορισμό

εμφανίζει μέγιστο όταν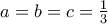
Και γιατί αγαπητέ Ανδρέα δεν παίρνει ελάχιστο ότανFriedoon έγραψε:Datis-Kalali έγραψε:Ανείναι θετικοί πραγματικοί αριθμοί,έτσι ώστε
να δείξετε οτι
Άρα αρκεί να δείξουμε ότι
Όμως,και
και
Άρα από
με
παίρνουμε πως η παράστασημε τον περιορισμό

εμφανίζει μέγιστο όταν
Άρα
και το ζητούμενο αποδείχθηκε.

Απαγορεύεται η χρήση των πολλαπλασιαστών Lagrange στον Αρχιμήδη;matha έγραψε:Επειδή μας παρακολουθούν μαθητές που θα συμμετάσχουν σε Διαγωνισμούς επιπέδου Αρχιμήδη και άνω, πρέπει να αναφέρουμε ότι μία τέτοια "λύση" βαθμολογείται με ΜΗΔΕΝ βαθμούς!Friedoon έγραψε:Datis-Kalali έγραψε:Ανείναι θετικοί πραγματικοί αριθμοί,έτσι ώστε
να δείξετε οτι
Άρα από
με
παίρνουμε πως η παράστασημε τον περιορισμό

εμφανίζει μέγιστο όταν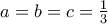
Όχι! Ωστόσο είναι μάλλον δύσκολο (όχι αδύνατο) να δικαιολογήσει κάποιος μαθητή με ορθότητα και πληρότητα τα επιχειρήματά του.Friedoon έγραψε:Απαγορεύεται η χρήση των πολλαπλασιαστών Lagrange στον Αρχιμήδη;matha έγραψε:Επειδή μας παρακολουθούν μαθητές που θα συμμετάσχουν σε Διαγωνισμούς επιπέδου Αρχιμήδη και άνω, πρέπει να αναφέρουμε ότι μία τέτοια "λύση" βαθμολογείται με ΜΗΔΕΝ βαθμούς!Friedoon έγραψε:
Άρα από
με
παίρνουμε πως η παράστασημε τον περιορισμό

εμφανίζει μέγιστο όταν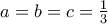
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες